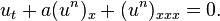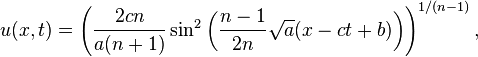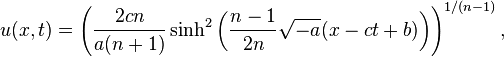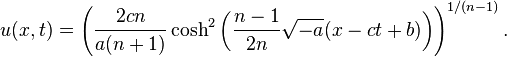Rosenau–Hyman equation

The Rosenau–Hyman equation or K(n,n) equation is a KdV-like equation having compacton solutions. This nonlinear partial differential equation is of the form[1]

u_t+a(u^n)_x+(u^n)_{xxx}=0. \,

The equation is named after Philip Rosenau and James M. Hyman, who used in their 1993 study of compactons.[2]

The K(n,n) equation has the following traveling wave solutions:

u(x,t)= \left( \frac{2cn}{a(n+1)} \sin^2 \left(\frac{n-1}{2n}\sqrt{a}(x-ct+b)\right)\right)^{1/(n-1)},
u(x,t)=\left( \frac{2cn}{a(n+1)}\sinh^2\left(\frac{n-1}{2n}\sqrt{-a}(x-ct+b)\right)\right)^{1/(n-1)},
u(x,t)= \left( \frac{2cn}{a(n+1)} \cosh^2 \left(\frac{n-1}{2n}\sqrt{-a}(x-ct+b)\right)\right)^{1/(n-1)}.

References

  1. ↑ Polyanin, Andrei D.; Zaitsev, Valentin F., Handbook of Nonlinear Partial Differential Equations (Second ed.), CRC Press, p. 891, ISBN 1584882972
  2. ↑ Rosenau, Philip; Hyman, James M. (1993), "Compactons: Solitons with finite wavelength", Physical Review Letters (American Physical Society) 70 (5): 564–567, Bibcode:1993PhRvL..70..564R, doi:10.1103/PhysRevLett.70.564
This article is issued from Wikipedia - version of the Friday, May 08, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.