Rokhlin lemma

In mathematics, the Rokhlin lemma, or Kakutani–Rokhlin lemma is an important result in ergodic theory. It states that an aperiodic measure preserving dynamical system can be decomposed to an arbitrary high tower of measurable sets and a remainder of arbitrarily small measure. It was proven by Vladimir Abramovich Rokhlin and independently by Shizuo Kakutani. The lemma is used extensively in ergodic theory, for example in Ornstein theory and has many generalizations.

Terminology

Rokhlin lemma belongs to the group mathematical statements such as Zorn's lemma in set theory and Schwarz lemma in complex analysis which are traditionally called lemmas despite the fact that their roles in their respective fields are fundamental.

Statement of the lemma

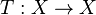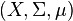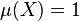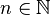Lemma: Let $\textstyle T:X\to X$ be an invertible measure-preserving transformation on a standard measure space $\textstyle (X,\Sigma,\mu)$ with $\textstyle \mu(X)=1$ . We assume $\textstyle T$ is aperiodic, that is, the set of periodic points for $\textstyle T$ has zero measure. 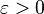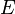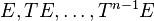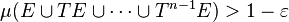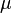Then for every integer $\textstyle n\in\mathbb{{N}}$ and for every $\textstyle \varepsilon>0$ , there exists a measurable set $\textstyle E$ such that the sets $\textstyle E,TE,\ldots,T^{n-1}E$ are pairwise disjoint and such that $\textstyle \mu(E\cup TE\cup\cdots\cup T^{n-1}E)>1-\varepsilon$

Remark: Note that if $\textstyle T$ is ergodic and $\textstyle \mu$ non-atomic, then the assumptions of the lemma hold.

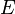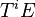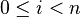A useful strengthening of the lemma states that given a finite measurable partition $\textstyle P$ , then $\textstyle E$ may be chosen in such a way that $\textstyle T^i E$ and $\textstyle P$ are independent for all $\textstyle 0\leq i<n$ .^[1]

A topological version of the lemma

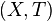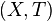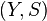Let $\textstyle (X,T)$ be a topological dynamical system consisting of a compact metric space $\textstyle X$ and a homeomorphism $\textstyle T:X\rightarrow X$ . The topological dynamical system $\textstyle (X,T)$ is called minimal if it has no proper non-empty closed $\textstyle T$ -invariant subsets. 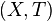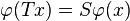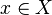A topological dynamical system $\textstyle (Y,S)$ is called a factor of $\textstyle (X,T)$ if there exists a continuous surjective mapping $\textstyle \varphi:X\rightarrow Y$ which is equivariant, i.e., $\textstyle \varphi(Tx)=S\varphi(x)$ for all $\textstyle x\in X$ .

Lindenstrauss proved the following theorem:^[2]

Theorem: Let 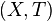$\textstyle (X,T)$ be a topological dynamical system which has an aperiodic minimal factor. Then for integer 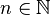$\textstyle n\in\mathbb{{N}}$ there is a continuous function 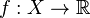$\textstyle f:X\rightarrow\mathbb{R}$ such that the set 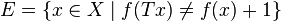$\textstyle E=\{x\in X\mid f(Tx)\neq f(x)+1\}$ satisfies 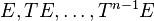$\textstyle E,TE,\ldots,T^{n-1}E$ are pairwise disjoint.

Further generalizations

There is a version for non-invertible measure preserving systems.^[3]
Ornstein and Weiss proved a version for free actions by countable discrete amenable groups.^[4]
C. Linderholm proved a version for periodic non-singular transformations.^[5]

References

↑ Shields, Paul (1973. Chicago Lectures in Mathematics.). The theory of Bernoulli shifts. The University of Chicago Press, Chicago, Ill.-London,. pp. Chapter 3. Check date values in: |date= (help)
↑ Lindenstrauss, Elon (1999-12-01). "Mean dimension, small entropy factors and an embedding theorem". Publications Mathématiques de l'Institut des Hautes Études Scientifiques 89 (1): 227–262. doi:10.1007/BF02698858. ISSN 0073-8301.
↑ "Isaac Kornfeld. Some old and new rokhlin towers. Contemporary Mathematics%2C 356%3A145%2C 2004. – Google Scholar". scholar.google.co.il. Retrieved 2015-09-21.
↑ Ornstein, Donald S.; Weiss, Benjamin (1987-12-01). "Entropy and isomorphism theorems for actions of amenable groups". Journal d’Analyse Mathématique 48 (1): 1–141. doi:10.1007/BF02790325. ISSN 0021-7670.
↑ Tulcea, A. Ionescu (1965-01-01). "On the Category of Certain Classes of Transformations in Ergodic Theory". Transactions of the American Mathematical Society 114 (1): 261–279. doi:10.2307/1994001.

Notes

V. Rokhlin. A "general" measure-preserving transformation is not mixing. Doklady Akad. Nauk SSSR (N.S.), 60:349–351, 1948.
Shizuo Kakutani. Induced measure preserving transformations. Proc. Imp. Acad. Tokyo, 19:635–641, 1943.
Benjamin Weiss. On the work of V. A. Rokhlin in ergodic theory. Ergodic Theory Dynam. Systems, 9(4):619–627, 1989.
Isaac Kornfeld. Some old and new rokhlin towers. Contemporary Mathematics, 356:145, 2004.