Roger Dashen
| Roger Dashen | |
|---|---|
| Born |
May 5, 1938 Grand Junction, Colorado |
| Died |
May 25, 1995 (aged 57) La Jolla, California |
| Nationality | American |
| Alma mater | CalTech |
| Known for | Quantum field theory |
Roger Frederick Dashen (May 5, 1938 in Grand Junction, Colorado - May 25, 1995 in La Jolla) was an American theoretical physicist who studied particle physics and quantum field theory.
Dashen studied physics at the Harvard University (where he also played in the football team), where he matriculated "summa cum laude" in 1960. Then he went to Caltech, where he earned his PhD in 1964. After that, he was a professor at Caltech in 1967 and the Institute for Advanced Study in 1969. In 1986 he became a professor at the University of California, San Diego (UCSD) in 1988 was Head of Faculty. He played a leading role in the establishment of a supercomputer center at UCSD and in the establishment of the Institute for Theoretical Physics of the National Science Foundation at the University of California, Santa Barbara.
In the 1960s he worked partly in collaboration with Murray Gell-Mann with current algebras of particle physics and models with chiral symmetry. With Steven Frautschi he tried 1964 Calculation of the mass difference of protons and neutrons within the S-matrix - theory, which is attributed to electromagnetic interactions.[1] In the 1970s, he studied with Brosl Hasslacher and André Neveu quantum field theoretical model theories (such as the Sine-Gordon model and the Gross-Neveu model) for extended particles and semiclassical approximations ([WKB approximation] []) for their analysis.[2] They developed the Dashen-Hasslacher-Neveu method (DHN) for quantization of solitons using path integrals. After the discovery of instantons in the quantum (QCD) by Polyakov, he examined it with David Gross and Curtis Callan.[3] In the 1980s, he worked with lattice gauge theory s and found with Neuberger (regardless of Giorgio Parisi) is an upper bound for the Higgs Boson - mass.[4]
Dashen was also involved in sound propagation in the ocean (with military applications in mind), where he applied quantum field theoretical methods (such as path integrals and the renormalization group) on the problem of random scattering of sound in the ocean. He worked with his JASON colleagues Kenneth Watson and Frederik Zachariason.[5] Dashen was senior scientific adviser to the US Navy, including the committee on the safety of SSBNs, the rocket-carrying submarines, and matters relating to submarine warfare. He was a member of the JASON Defense Advisory Group.
Dashen was a member of the National Academy of Sciences since 1984.
He was married and had two daughters.
Books
- Roger Dashen and Steve Adler: Current Algebras. Applications to Particle Physics . Benjamin 1968
References
- ↑ Dashen and Frautschi. S-Matrix Method for Calculating electromagnetic corrections to strong interactions . In: Physical Review B . Band 135, 1964, 1190
- ↑ Dashen, Hasslacher and Neveu. non perturbative Models and extended hadron models in field theory Part 1 Semi Classical Functional Methods . In: Physical Review D . Volume 10, 1974, p 4114, Part 2 Two dimensional models and extended hadrons . In: Physical Review D . Volume 10, 1974, p.4 130; The Particle Spectrum in Model Field Theories from semiclassical functional integral techniques . In: Physical Review D . Volume 11, 1975, p 3424; Semi Classical bound states in asymptotically free theory on . In: Physical Review D . Volume 12, 1975, p 2443
- ↑ Callan, Dashen and Gross: The structure of the vacuum gauge theory . In: Physics Letters B . Volume 63, 1976, p 334; Toward a theory of the strong interactions . In: Physical Review D . Volume 17, 1979, p 2717
- ↑ From the assumed triviality of
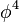 theories.. Et al According to later work of Kuti, Lee, Shen is the consequent upper limit in the Glashow-Weinberg-Salam theory (standard model of electroweak interactions) at 700 GeV.
theories.. Et al According to later work of Kuti, Lee, Shen is the consequent upper limit in the Glashow-Weinberg-Salam theory (standard model of electroweak interactions) at 700 GeV. - ↑ Dashen, Watson, Zachariason, Walter Munk and Stanley Flatte. Propagating sound in a fluctuating ocean . Cambridge University Press, 1979
External links
|