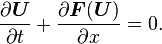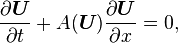Roe solver
The Roe approximate Riemann solver, devised by Phil Roe, is an approximate Riemann solver based on the Godunov scheme and involves finding an estimate for the intercell numerical flux or Godunov flux 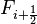 at the interface between two computational cells
at the interface between two computational cells 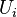 and
and 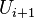 , on some discretised space-time computational domain.
, on some discretised space-time computational domain.
The Roe Scheme
Quasi-linear Hyperbolic system
A non-linear system of hyperbolic partial differential equations representing a set of conservation laws in one spatial dimension can be written in the form
Applying the chain rule to the second term we get the quasi-linear hyperbolic system
where  is the jacobian matrix of the flux vector
is the jacobian matrix of the flux vector 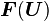 .
.
The Roe Matrix
The Roe method consists of finding a matrix 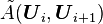 that is assumed constant between two cells. The Riemann problem can then be solved as a truly linear hyperbolic system at each cell interface. The Roe matrix must obey the following conditions:
that is assumed constant between two cells. The Riemann problem can then be solved as a truly linear hyperbolic system at each cell interface. The Roe matrix must obey the following conditions:
- Diagonalizable with real eigenvalues Ensures that the new linear system is truly hyperbolic.
- Consistency with the exact jacobian When
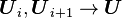 we demand that
we demand that 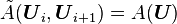
- Conserving
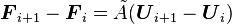
Phil Roe introduced a method of parameter vectors[1] to find such a matrix for some systems of conservation laws.
The Intercell Flux
Once the Roe matrix corresponding to the interface between two cells is found, the intercell flux is given by solving the quasi-linear system as a truly linear system.
References
- ↑ P. L. Roe, Approximate riemann solvers, parameter vectors and difference schemes, Journal of Computational Physics, 43, 357-372, (1981)
Further reading
- Toro, E. F. (1999), Riemann Solvers and Numerical Methods for Fluid Dynamics, Springer-Verlag.