RiskMetrics

Not to be confused with risk metric, the abstract concept quantified by risk measures.

The RiskMetrics variance model (also known as exponential smoother) was first established in 1989, when Sir Dennis Weatherstone, the new chairman of J.P. Morgan, asked for a daily report measuring and explaining the risks of his firm. Nearly four years later in 1992, J.P. Morgan launched the RiskMetrics methodology to the marketplace, making the substantive research and analysis that satisfied Sir Dennis Weatherstone's request freely available to all market participants.

In 1998, as client demand for the group's risk management expertise exceeded the firm's internal risk management resources, the Corporate Risk Management Department was spun off from J.P. Morgan as RiskMetrics Group with 23 founding employees. The RiskMetrics technical document was revised in 1996. In 2001, it was revised again in Return to RiskMetrics. In 2006, a new method for modeling risk factor returns was introduced (RM2006). On 25 January 2008, RiskMetrics Group listed on the New York Stock Exchange (NYSE: RISK). In June 2010, RiskMetrics was acquired by MSCI.

Risk measurement process

Portfolio risk measurement can be broken down into steps. The first is modeling the market that drives changes in the portfolio's value. The market model must be sufficiently specified so that the portfolio can be revalued using information from the market model. The risk measurements are then extracted from the probability distribution of the changes in portfolio value. The change in value of the portfolio is typically referred to by portfolio managers as profit and loss, or P&L

Risk factors

Risk management systems are based on models that describe potential changes in the factors affecting portfolio value. These risk factors are the building blocks for all pricing functions. In general, the factors driving the prices of financial securities are equity prices, foreign exchange rates, commodity prices, interest rates, correlation and volatility. By generating future scenarios for each risk factor, we can infer changes in portfolio value and reprice the portfolio for different "states of the world".

Portfolio risk measures

Standard deviation

The first widely used portfolio risk measure was the standard deviation of portfolio value, as described by Harry Markowitz. While comparatively easy to calculate, standard deviation is not an ideal risk measure since it penalizes profits as well as losses.

Value at risk

The 1994 tech doc popularized VaR as the risk measure of choice among investment banks looking to be able to measure their portfolio risk for the benefit of banking regulators. VaR is a downside risk measure, meaning that it typically focuses on losses.

Expected shortfall

A third commonly used risk measure is expected shortfall, also known variously as expected tail loss, XLoss, conditional VaR, or CVaR.

Marginal VaR

The Marginal VaR of a position with respect to a portfolio can be thought of as the amount of risk that the position is adding to the portfolio. It can be formally defined as the difference between the VaR of the total portfolio and the VaR of the portfolio without the position.

To measure the effect of changing positions on portfolio risk, individual VaRs are insufficient. Volatility measures the uncertainty in the return of an asset, taken in isolation. When this asset belongs to a portfolio, however, what matters is the contribution to portfolio risk.

— Philippe Jorion (2007)

Incremental risk

Incremental risk statistics provide information regarding the sensitivity of portfolio risk to changes in the position holding sizes in the portfolio.

An important property of incremental risk is subadditivity. That is, the sum of the incremental risks of the positions in a portfolio equals the total risk of the portfolio. This property has important applications in the allocation of risk to different units, where the goal is to keep the sum of the risks equal to the total risk.

Since there are three risk measures covered by RiskMetrics, there are three incremental risk measures: Incremental VaR (IVaR), Incremental Expected Shortfall (IES), and Incremental Standard Deviation (ISD).

Incremental statistics also have applications to portfolio optimization. A portfolio with minimum risk will have incremental risk equal to zero for all positions. Conversely, if the incremental risk is zero for all positions, the portfolio is guaranteed to have minimum risk only if the risk measure is subadditive.

Coherent risk measures

A coherent risk measure satisfies the following four properties:

1. Subadditivity

A risk measure is subadditive if for any portfolios A and B, the risk of A+B is never greater than the risk of A plus the risk of B. In other words, the risk of the sum of subportfolios is smaller than or equal to the sum of their individual risks.

Standard deviation and expected shortfall are subadditive, while VaR is not.

Subadditivity is required in connection with aggregation of risks across desks, business units, accounts, or subsidiary companies. This property is important when different business units calculate their risks independently and we want to get an idea of the total risk involved. Subadditivity could also be a matter of concern for regulators, where firms might be motivated to break up into affiliates to satisfy capital requirements.

2. Translation invariance

Adding cash to the portfolio decreases its risk by the same amount.

3. Positive homogeneity of degree 1

If we double the size of every position in a portfolio, the risk of the portfolio will be twice as large.

4. Monotonicity

If losses in portfolio A are larger than losses in portfolio B for all possible risk factor return scenarios, then the risk of portfolio A is higher than the risk of portfolio B.

Assessing risk measures

The estimation process of any risk measure can be wrong by a considerable margin. If from the imprecise estimate we cannot get a good understanding what the true value could be, then the estimate is virtually worthless. A good risk measurement is to supplement any estimated risk measure with some indicator of their precision, or, of the size of its error.

There are various ways to quantify the error of some estimates. One approach is to estimate a confidence interval of the risk measurement.

Market models

RiskMetrics describes three models for modeling the risk factors that define financial markets.

Covariance approach

The first is very similar to the mean-covariance approach of Markowitz. Markowitz assumed that asset covariance matrix 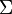\Sigma can be observed. The covariance matrix can be used to compute portfolio variance. RiskMetrics assumes that the market is driven by risk factors with observable covariance. The risk factors are represented by time series of prices or levels of stocks, currencies, commodities, and interest rates. Instruments are evaluated from these risk factors via various pricing models. The portfolio itself is assumed to be some linear combination of these instruments.

Historical simulation

The second market model assumes that the market only has finitely many possible changes, drawn from a risk factor return sample of a defined historical period. Typically one performs a historical simulation by sampling from past day-on-day risk factor changes, and applying them to the current level of the risk factors to obtain risk factor price scenarios. These perturbed risk factor price scenarios are used to generate a profit (loss) distribution for the portfolio.

This method has the advantage of simplicity, but as a model, it is slow to adapt to changing market conditions. It also suffers from simulation error, as the number of simulations is limited by the historical period (typically between 250 and 500 business days).

Monte carlo simulation

The third market model assumes that the logarithm of the return, or, log-return, of any risk factor typically follows a normal distribution. Collectively, the log-returns of the risk factors are multivariate normal. Monte Carlo simulation generates random market scenarios drawn from that multivariate normal distribution. For each scenario, the profit (loss) of the portfolio is computed. This collection of profit (loss) scenarios provides a sampling of the profit (loss) distribution from which one can compute the risk measures of choice.

See also

References

External links

This article is issued from Wikipedia - version of the Thursday, December 17, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.