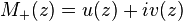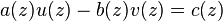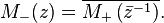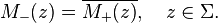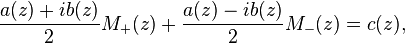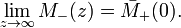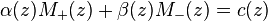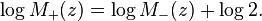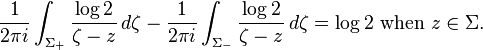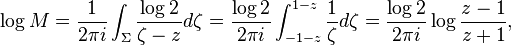Riemann–Hilbert problem

For the original problem of Hilbert concerning the existence of linear differential equations having a given monodromy group see Hilbert's twenty-first problem.

In mathematics, Riemann–Hilbert problems, named after Bernhard Riemann and David Hilbert, are a class of problems that arise in the study of differential equations in the complex plane. Several existence theorems for Riemann–Hilbert problems have been produced by Krein, Gohberg and others (see the book by Clancey and Gohberg (1981)).

The Riemann problem

Suppose that Σ is a closed simple contour in the complex plane dividing the plane into two parts denoted by Σ₊ (the inside) and Σ₋ (the outside), determined by the index of the contour with respect to a point. The classical problem, considered in Riemann's PhD dissertation (see Pandey (1996)), was that of finding a function

M_+(z) = u(z) + i v(z)\!

analytic inside Σ₊ such that the boundary values of M₊ along Σ satisfy the equation

a(z)u(z) - b(z)v(z) = c(z) \!

for all z ∈ Σ, where a, b, and c are given real-valued functions (Bitsadze 2001).

By the Riemann mapping theorem, it suffices to consider the case when Σ is the unit circle (Pandey 1996, §2.2). In this case, one may seek M₊(z) along with its Schwarz reflection:

M_-(z) = \overline{M_+\left(\bar{z}^{-1}\right)}.

On the unit circle Σ, one has 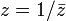$z = 1/\bar{z}$ , and so

M_-(z) = \overline{M_+(z)},\quad z\in\Sigma.

Hence the problem reduces to finding a pair of functions M₊(z) and M₋(z) analytic, respectively, on the inside and the outside of the unit disc, so that on the unit circle

\frac{a(z)+ib(z)}{2}M_+(z) + \frac{a(z)-ib(z)}{2}M_-(z) = c(z),

and, moreover, so that the condition at infinity holds:

\lim_{z\to\infty}M_-(z) = \bar{M}_+(0).

The Hilbert problem

Hilbert's generalization was to consider the problem of attempting to find M₊ and M_- analytic, respectively, on the inside and outside of the curve Σ, such that on Σ one has

\alpha(z) M_+(z) + \beta(z) M_-(z) = c(z)\,

where α, β, and c are arbitrary given complex-valued functions (no longer just complex conjugates).

Riemann–Hilbert problems

In the Riemann problem as well as Hilbert's generalization, the contour Σ was simple. A full Riemann–Hilbert problem allows that the contour may be composed of a union of several oriented smooth curves, with no intersections. The + and − sides of the "contour" may then be determined according to the index of a point with respect to Σ. The Riemann–Hilbert problem is to find a pair of functions, M₊ and M₋ analytic, respectively, on the + and − side of Σ, subject to the equation

\alpha(z) M_+(z) + \beta(z) M_-(z) = c(z)\,

for all z∈Σ.

Generalization: factorization problems

Given an oriented "contour" Σ (technically: an oriented union of smooth curves without points of infinite self-intersection in the complex plane). A Birkhoff factorization problem is the following.

Given a matrix function V defined on the contour Σ, to find a holomorphic matrix function M defined on the complement of Σ, such that two conditions be satisfied:

If M₊ and M₋ denote the non-tangential limits of M as we approach Σ, then M₊ = M₋V, at all points of non-intersection in Σ.
As z tends to infinity along any direction outside Σ, M tends to the identity matrix.

In the simplest case V is smooth and integrable. In more complicated cases it could have singularities. The limits M₊ and M₋ could be classical and continuous or they could be taken in the L₂ sense.

Applications to integrability theory

Riemann–Hilbert problems have applications to several related classes of problems.

A. Integrable models. The inverse scattering or inverse spectral problem associated to the Cauchy problem for 1+1 dimensional partial differential equations on the line, periodic problems, or even initial-boundary value problems, can be stated as Riemann–Hilbert problems.

B. Orthogonal polynomials, Random matrices. Given a weight on a contour, the corresponding orthogonal polynomials can be computed via the solution of a Riemann–Hilbert factorization problem. Furthermore, the distribution of eigenvalues of random matrices in several ensembles is reduced to computations involving orthogonal polynomials (see for example Deift (1999)).

C. Combinatorial probability. The most celebrated example is the theorem of Baik, Deift & Johansson (1999) on the distribution of the length of the longest increasing subsequence of a random permutation.

In particular, Riemann–Hilbert factorization problems are used to extract asymptotics for the three problems above (say, as time goes to infinity, or as the dispersion coefficient goes to zero, or as the polynomial degree goes to infinity, or as the size of the permutation goes to infinity). There exists a method for extracting the asymptotic behavior of solutions of Riemann–Hilbert problems, analogous to the method of stationary phase and the method of steepest descent applicable to exponential integrals.

By analogy with the classical asymptotic methods, one "deforms" Riemann–Hilbert problems which are not explicitly solvable to problems that are. The so-called "nonlinear" method of stationary phase is due to Deift & Zhou (1993), expanding on a previous idea by Its (1982) and Manakov (1979). A crucial ingredient of the Deift–Zhou analysis is the asymptotic analysis of singular integrals on contours.

An essential extension of the nonlinear method of stationary phase has been the introduction of the so-called finite gap g-function transformation by Deift, Venakides & Zhou (1997), which has been crucial in most applications. This was inspired by work of Lax, Levermore and Venakides, who reduced the analysis of the small dispersion limit of the KdV equation to the analysis of a maximization problem for a logarithmic potential under some external field: a variational problem of "electrostatic" type. The g-function is the logarithmic transform of the maximizing "equilibrium" measure. The analysis of the small dispersion limit of KdV has in fact provided the basis for the analysis of most of the work concerning "real" orthogonal polynomials (i.e. with the orthogonality condition defined on the real line) and Hermitian random matrices.

Perhaps the most sophisticated extension of the theory so far is the one applied to the "non self-adjoint" case, i.e. when the underlying Lax operator (the first component of the Lax pair) is not self-adjoint, by Kamvissis, McLaughlin & Miller (2003). In that case, actual "steepest descent contours" are defined and computed. The corresponding variational problem is a max-min problem: one looks for a contour that minimizes the "equilibrium" measure. The study of the variational problem and the proof of a regular solution, under some conditions on the external field, was done in Kamvissis & Rakhmanov (2005).

An alternative asymptotic analysis of Riemann–Hilbert factorization problems is provided in McLaughlin & Miller (2006), especially convenient when jump matrices do not have analytic extensions. Their method is based on the analysis of d-bar problems, rather than the asymptotic analysis of singular integrals on contours. An alternative way of dealing with jump matrices with no analytic extensions was introduced in Varzugin (1996).

Another extension of the theory appears in Kamvissis & Teschl (2012) where the underlying space of the Riemann–Hilbert problem is a compact hyperelliptic Riemann surface. The right factorization problem is no more holomorphic, but rather meromorphic, by reason of the Riemann–Roch theorem. The Riemann–Hilbert problem deformation theory is applied to the problem of stability of the infinite periodic Toda lattice under a "short range" perturbation (for example a perturbation of a finite number of particles).

Most Riemann–Hilbert factorization problems studied in the literature are 2-dimensional, i.e. the unknown matrices are of dimension 2. Higher-dimensional problems have been studied by Kuijlaars and collaborators, see e.g. Kuijlaars & López (2014).

Example: Scalar Riemann–Hilbert factorization problem

Suppose V = 2, and Σ is a contour from z = −1 to z = 1. What is the solution of M?

To solve this, let's take the logarithm of equation 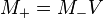$M_+=M_- V$ .

\log M_+(z) = \log M_-(z) + \log 2.

Since M tends to 1, log M tends to zero as z tends to infinity.

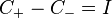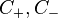A standard fact about the Cauchy transform is that $C_+ -C_- = I$ where $C_+ , C_-$ are the limits of the Cauchy transform from above and below Σ; therefore, we get

\frac{1}{2\pi i}\int_{\Sigma_+} \frac{\log 2}{\zeta-z} \, d\zeta - \frac{1}{2\pi i} \int_{\Sigma_-} \frac{\log{2}}{\zeta-z} \, d\zeta = \log 2 \text{ when } z\in\Sigma.

Because the solution M of a Riemann–Hilbert factorization problem is unique (an easy application of Liouville's theorem (complex analysis)), the Sokhotski–Plemelj theorem gives the solution. We get

\log M = \frac{1}{2\pi i}\int_{\Sigma}\frac{\log{2}}{\zeta-z}d\zeta = \frac{\log 2}{2\pi i}\int^{1-z}_{-1-z}\frac{1}{\zeta}d\zeta = \frac{\log 2}{2\pi i} \log{\frac{z-1}{z+1}},

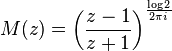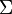i.e. $M(z)=\left( \frac{z-1}{z+1} \right)^{\frac{\log{2}}{2\pi i}}$ which has a branch cut at contour $\Sigma$ .

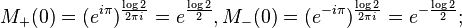
Check: $M_+(0) =(e^{i\pi})^{\frac{\log 2}{2\pi i}} = e^{\frac{\log 2}{2}}, M_-(0) =(e^{-i\pi})^{\frac{\log 2}{2\pi i}} = e^{-\frac{\log 2}{2}};$

therefore, 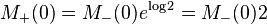$M_+(0)=M_-(0)e^{\log{2}}=M_-(0)2$ .

CAVEAT: If the problem is not scalar one cannot take logarithms. In general explicit solutions are very rare.

References

Baik, J.; Deift, P.; Johansson, K. (1999), "On the distribution of the length of the longest increasing subsequence of random permutations", J. Amer. Math. Soc. 12: 1119–1178 .

Bitsadze, A.V. (2001), "Boundary value problems of analytic function theory", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

Clancey, K.; Gohberg, I. (1981), Factorization of matrix functions and singular integral operators, Oper. Theory: Advances and Appl. 3, Basel-Boston-Stuttgart: Birkhäuser Verlag .

Deift, P. A. (2000), Orthogonal Polynomials and Random Matrices, AMS, ISBN 978-0-8218-2695-9 .

Deift, P.; Venakides, S.; Zhou, X. (1997), New Results in Small Dispersion KdV by an Extension of the Steepest Descent Method for Riemann–Hilbert Problems, International Mathematical Research Notices, pp. 286–299 .

Deift, P.; Zhou, X. (1993), "A Steepest Descent Method for Oscillatory Riemann–Hilbert Problems; Asymptotics for the MKdV Equation", Annals of Mathematics, Second Series 137 (2): 295–368, doi:10.2307/2946540 .

Khimshiashvili, G. (2001), "Birkhoff factorization", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 .

Its, A.R. (1982), "Asymptotics of Solutions of the Nonlinear Schrödinger Equation and Isomonodromic Deformations of Systems of Linear Differential Equations", Soviet Mathematics Doklady 24 (3): 14–18 .

Its, A.R. (2003), "The Riemann–Hilbert Problem and Integrable Systems" (PDF), Notices of the AMS 50 (11): 1389–1400 .

Kamvissis, S.; McLaughlin, K.; Miller, P. (2003), Semiclassical Soliton Ensembles for the Focusing Nonlinear Schrödinger Equation, Annals of Mathematics (Study 154), Princeton: Princeton University Press .

Kamvissis, S.; Rakhmanov, E.A. (2005), "Existence and Regularity for an Energy Maximization Problem in Two Dimensions", J.Math.Phys 46 (8): 083505, Bibcode:2005JMP....46h3505K, doi:10.1063/1.1985069 .

Kamvissis, S.; Teschl, G. (2012), "Long-time asymptotics of the periodic Toda lattice under short-range perturbations", J.Math.Phys 53 (7): 073706, arXiv:0705.0346, Bibcode:2012JMP....53g3706K, doi:10.1063/1.4731768 .

Kuijlaars, Arno; López, Abey, A vector equilibrium problem for the normal matrix model, and multiple orthogonal polynomials on a star, arXiv:1401.2419 .

Lax, P.D.; Levermore, C.D. (1983), "The Zero Dispersion Limit for the KdV Equation I-III", Communications on Pure and Applied Mathematics 36: 253–290, 571–593, 809–829 .

Manakov, S.V. (1974), "Nonlinear Fraunnhofer diffraction", Sov. Phys. JETP 38: 693–696, Bibcode:1974JETP...38..693M .

McLaughlin, K.; Miller, P. (2006), "The d-bar steepest descent method and the asymptotic behavior of polynomials orthogonal on the unit circle with fixed and exponentially varying nonanalytic weights", IMRP: 1–77 .

Pandey, J.N. (1996), The Hilbert transform of Schwartz distributions and applications, Wiley-Interscience .

Varzugin, G.G. (1996), "Asymptotics of oscillatory Riemann-Hilbert problems", J.Math.Phys 37 (11) .

External links

Gakhov, F.D. (2001), "Riemann–Hilbert problem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

This article is issued from Wikipedia - version of the Friday, February 12, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.