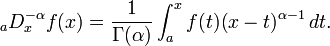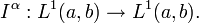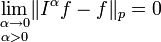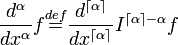Riemann–Liouville integral

Part of a series of articles about

Definitions
Derivative (generalizations) Differential infinitesimal of a function total
Concepts
Differentiation notation Second derivative Third derivative Change of variables Implicit differentiation Related rates Taylor's theorem
Rules and identities
Sum Product Chain Power Quotient Faà di Bruno's formula

Integral

Definitions
Lists of integrals
Antiderivative Integral (improper) Riemann integral Lebesgue integration Contour integration
Integration by
Parts Discs Cylindrical shells Substitution (trigonometric) Partial fractions Order Reduction formulae

Series

Convergence tests
Geometric (arithmetico-geometric) Harmonic Alternating Power Binomial Taylor
Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel

Vector

Theorems
Gradient Divergence Curl Laplacian Directional derivative Identities
Divergence Gradient Green's Stokes'

Multivariable

Formalisms
Matrix Tensor Exterior Geometric
Definitions
Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian Hessian matrix

Specialized

In mathematics, the Riemann–Liouville integral associates with a real function ƒ : R → R another function I^αƒ of the same kind for each value of the parameter α > 0. The integral is a manner of generalization of the repeated antiderivative of ƒ in the sense that for positive integer values of α, I^αƒ is an iterated antiderivative of ƒ of order α. The Riemann–Liouville integral is named for Bernhard Riemann and Joseph Liouville, the latter of whom was the first to consider the possibility of fractional calculus in 1832.^[1] The operator agrees with the Euler transform, after Leonhard Euler, when applied to analytic functions.^[2] It was generalized to arbitrary dimensions by Marcel Riesz, who introduced the Riesz potential.

Definition

The Riemann–Liouville integral is defined by

I^\alpha f(x) = \frac{1}{\Gamma(\alpha)}\int_a^xf(t)(x-t)^{\alpha-1}\,dt

where Γ is the Gamma function and a is an arbitrary but fixed base point. The integral is well-defined provided ƒ is a locally integrable function, and α is a complex number in the half-plane re(α) > 0. The dependence on the base-point a is often suppressed, and represents a freedom in constant of integration. Clearly I¹ƒ is an antiderivative of ƒ (of first order), and for positive integer values of α, I^αƒ is an antiderivative of order α by Cauchy formula for repeated integration. Another notation, which emphasizes the basepoint, is^[3]

{}_aD_x^{-\alpha}f(x) = \frac{1}{\Gamma(\alpha)}\int_a^x f(t)(x-t)^{\alpha-1}\,dt.

This also makes sense if a = −∞, with suitable restrictions on ƒ.

The fundamental relations hold

\frac{d}{dx}I^{\alpha+1} f(x) = I^\alpha f(x),\quad I^\alpha(I^\beta f) = I^{\alpha+\beta}f,

the latter of which is a semigroup property.^[1] These properties make possible not only the definition of fractional integration, but also of fractional differentiation, by taking enough derivatives of I^αƒ.

Properties

Fix a bounded interval (a,b). The operator I^α associates to each integrable function ƒ on (a,b) the function I^αƒ on (a,b) which is also integrable by Fubini's theorem. Thus I^α defines a linear operator on L¹(a,b):

I^\alpha : L^1(a,b) \to L^1(a,b).

Fubini's theorem also shows that this operator is continuous with respect to the Banach space structure on L¹, and that the following inequality holds:

\|I^\alpha f\|_1 \le \frac{|b-a|^{\operatorname{re}(\alpha)}}{\operatorname{re}(\alpha)|\Gamma(\alpha)|}\|f\|_1.

Here $\|\cdot\|_1$ denotes the norm on L¹(a,b).

More generally, by Hölder's inequality, it follows that if ƒ ∈ L^p(a,b), then I^αƒ ∈ L^p(a,b) as well, and the analogous inequality holds

\|I^\alpha f\|_p \le \frac{|b-a|^{\operatorname{re}(\alpha)/p}}{\operatorname{re}(\alpha)|\Gamma(\alpha)|}\|f\|_p

where $\|\cdot\|_p$ is the L^p norm on the interval (a,b). Thus I^α defines a bounded linear operator from L^p(a,b) to itself. Furthermore, I^αƒ tends to ƒ in the L^p sense as α → 0 along the real axis. That is

\underset{\alpha > 0}{\lim_{\alpha\to 0}} \|I^\alpha f-f\|_p = 0

for all p ≥ 1. Moreover, by estimating the maximal function of I, one can show that the limit I^αƒ → ƒ holds pointwise almost everywhere.

The operator I^α is well-defined on the set of locally integrable function on the whole real line R. It defines a bounded transformation on any of the Banach spaces of functions of exponential type X_σ = L¹(e^-σ|t|dt), consisting of locally integrable functions for which the norm

\|f\| = \int_{-\infty}^\infty |f(t)|e^{-\sigma|t|}\,dt

is finite. For ƒ in X_σ, the Laplace transform of I^αƒ takes the particularly simple form

(\mathcal{L}I^\alpha f)(s) = s^{-\alpha}F(s)

for re(s) > σ. Here F(s) denotes the Laplace transform of ƒ, and this property expresses that I^α is a Fourier multiplier.

Fractional derivatives

One can define fractional-order derivatives of ƒ as well by

\frac{d^\alpha}{dx^\alpha} f \overset{def}{=} \frac{d^{\lceil\alpha\rceil}}{dx^{\lceil\alpha\rceil}} I^{\lceil\alpha\rceil-\alpha}f

where $\lceil\cdot\rceil$ denotes the ceiling function. One also obtains a differintegral interpolating between differentiation and integration by defining

D^\alpha_x f(x) = \begin{cases} \frac{d^{\lceil\alpha\rceil}}{dx^{\lceil\alpha\rceil}} I^{\lceil\alpha\rceil-\alpha}f(x)& \alpha>0\\ f(x) & \alpha=0\\ I^{-\alpha}f(x) & \alpha<0. \end{cases}

An alternative fractional derivative was introduced by Caputo in 1967, and produces a derivative that has different properties: it produces zero from constant functions and, more importantly, the initial value terms of the Laplace Transform are expressed by means of the values of that function and of its derivative of integer order rather than the derivatives of fractional order as in the Riemann–Liouville derivative. The Caputo fractional derivative with base point $x$ , is then:

D_x^{\alpha}f(y)=\frac{1}{\Gamma(1-\alpha)}\int_x^y f'(y-u)(u-x)^{-\alpha}du.

Another representation is:

{}_a\tilde{D}^\alpha_x f(x)=I^{\lceil \alpha\rceil-\alpha}\left(\frac{d^{\lceil \alpha\rceil}f}{dx^{\lceil \alpha\rceil}}\right).

Notes

References

Brychkov, Yu.A.; Prudnikov, A.P. (2001), "Euler transformation", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 .
Hille, Einar; Phillips, Ralph S. (1974), Functional analysis and semi-groups, Providence, R.I.: American Mathematical Society, MR 0423094 .
Lizorkin, P.I. (2001), "Fractional integration and differentiation", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 .
Miller, Kenneth S.; Ross, Bertram (1993), An Introduction to the Fractional Calculus and Fractional Differential Equations, John Wiley & Sons, ISBN 0-471-58884-9 .
Riesz, Marcel (1949), "L'intégrale de Riemann-Liouville et le problème de Cauchy", Acta Mathematica 81 (1): 1–223, doi:10.1007/BF02395016, ISSN 0001-5962, MR 0030102 .

External links

Alan Beardon (2000). "Fractional calculus II". University of Cambridge.
Alan Beardon (2000). "Fractional calculus III". University of Cambridge.

This article is issued from Wikipedia - version of the Friday, November 13, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.