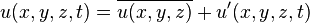Reynolds decomposition

In fluid dynamics and the theory of turbulence, Reynolds decomposition is a mathematical technique to separate the average and fluctuating parts of a quantity. For example, for a quantity the decomposition would be

where denotes the time average of (often called the steady component), and 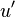the fluctuating part (or perturbations). The perturbations are defined such that their time average equals zero. ^[1]

This allows us to simplify the Navier–Stokes equations by substituting in the sum of the steady component and perturbations to the velocity profile and taking the mean value. The resulting equation contains a nonlinear term known as the Reynolds stresses which gives rise to turbulence.

See also

• Reynolds-averaged Navier–Stokes equations
• Turbulence

References