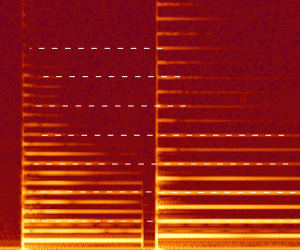
Acoustic resonance

This article is about mechanical resonance of sound including musical instruments. For a general description of mechanical resonance in physics and engineering, see mechanical resonance. For a general description of resonance, see resonance.

Acoustic resonance is a phenomenon that consists of a given acoustic system amplifying a sound whose frequency matches one of its own natural frequencies of vibration (its resonance frequencies).

The term "acoustic resonance" is sometimes used to narrow mechanical resonance to the frequency range of human hearing, but since acoustics is defined in general terms concerning vibrational waves in matter [1] acoustic resonance can occur at frequencies outside the range of human hearing.

An acoustically resonant object usually has more than one resonance frequency, especially at harmonics of the strongest resonance. It will easily vibrate at those frequencies, and vibrate less strongly at other frequencies. It will "pick out" its resonance frequency from a complex excitation, such as an impulse or a wideband noise excitation. In effect, it is filtering out all frequencies other than its resonance.

Acoustic resonance is an important consideration for instrument builders, as most acoustic instruments use resonators, such as the strings and body of a violin, the length of tube in a flute, and the shape of a drum membrane. Acoustic resonance is also important for hearing. For example, resonance of a stiff structural element, called the basilar membrane within the cochlea of the inner ear allows hair cells on the membrane to detect sound. (For mammals the membrane has tapering resonances across its length so that high frequencies are concentrated on one end and low frequencies on the other.)

Like mechanical resonance, acoustic resonance can result in catastrophic failure of the vibrator. The classic example of this is breaking a wine glass with sound at the precise resonant frequency of the glass; although this is difficult in practice.[2][3]

Resonance of a string

String resonance of a bass guitar A note with fundamental frequency of 110 Hz. Computed with from sampled sound with https://sourceforge.net/projects/amoreaccuratefouriertransform/ .

Strings under tension, as in instruments such as lutes, harps, guitars, pianos, violins and so forth, have resonant frequencies directly related to the mass, length, and tension of the string. The wavelength that will create the first resonance on the string is equal to twice the length of the string. Higher resonances correspond to wavelengths that are integer divisions of the fundamental wavelength. The corresponding frequencies are related to the speed v of a wave traveling down the string by the equation

f = {nv \over 2L}

where L is the length of the string (for a string fixed at both ends) and n = 1, 2, 3...(Harmonic in an open end pipe (that is, both ends of the pipe are open)). The speed of a wave through a string or wire is related to its tension T and the mass per unit length ρ:

v = \sqrt {T \over \rho}

So the frequency is related to the properties of the string by the equation

f = {n\sqrt {T \over \rho} \over 2 L} = {n\sqrt {T \over m / L} \over 2 L}

where T is the tension, ρ is the mass per unit length, and m is the total mass.

Higher tension and shorter lengths increase the resonant frequencies. When the string is excited with an impulsive function (a finger pluck or a strike by a hammer), the string vibrates at all the frequencies present in the impulse (an impulsive function theoretically contains 'all' frequencies). Those frequencies that are not one of the resonances are quickly filtered out—they are attenuated—and all that is left is the harmonic vibrations that we hear as a musical note.

String resonance in music instruments

String resonance occurs on string instruments. Strings or parts of strings may resonate at their fundamental or overtone frequencies when other strings are sounded. For example, an A string at 440 Hz will cause an E string at 330 Hz to resonate, because they share an overtone of 1320 Hz (3rd overtone of A and 4th overtone of E).

Resonance of a tube of air

The resonance of a tube of air is related to the length of the tube, its shape, and whether it has closed or open ends. Musically useful tube shapes are conical and cylindrical (see bore). A pipe that is closed at one end is said to be stopped while an open pipe is open at both ends. Modern orchestral flutes behave as open cylindrical pipes; clarinets and lip-reed instruments (brass instruments) behave as closed cylindrical pipes; and saxophones, oboes, and bassoons as closed conical pipes.[4] Vibrating air columns also have resonances at harmonics, like strings.

Cylinders

By convention a rigid cylinder that is open at both ends is referred to as an "open" cylinder, whereas a rigid cylinder that is open at one end and has a rigid surface at the other end is referred to as a "closed" cylinder.

The first three resonances in an open cylindrical tube. The horizontal axis is pressure.
The first three resonances in a one end open and other end closed cylindrical tube. The horizontal axis is pressure.

Open

An open tube is a tube in which both ends are open. The tube resonates at many frequencies or notes. Its lowest resonance (called its fundamental frequency) occurs at the same frequency as a closed tube of half its length. An open tube will resonate if there is a displacement antinode at each open end. These displacement antinodes are places where there is a maximum movement of air in and out of the ends of the tube. By overblowing an open tube, a note can be obtained that is an octave above the fundamental frequency or note of the tube. For example, if the fundamental note of an open pipe is C1, then overblowing the pipe gives C2, which is an octave above C1.[5]

Open cylindrical tubes resonate at the approximate frequencies:

f = {nv \over 2L}

where n is a positive integer (1, 2, 3...) representing the resonance node, L is the length of the tube and v is the speed of sound in air (which is approximately 343 metres per second [770 mph] at 20 °C [68 °F] and at sea level).

A more accurate equation considering an end correction is given below:

f = {nv \over 2(L+0.8d)}

where d is the diameter of the resonance tube. This equation compensates for the fact that the exact point at which a sound wave is reflecting at an open end is not perfectly at the end section of the tube, but a small distance outside the tube.


The reflection ratio is slightly less than 1; the open end does not behave like an infinitesimal acoustic impedance; rather, it has a finite value, called radiation impedance, which is dependent on the diameter of the tube, the wavelength, and the type of reflection board possibly present around the opening of the tube.

So when n is 1:

f = {v \over 2(L+0.8d)}
{f(2(L+0.8d))} = v
{f\lambda} = v
\lambda = {2(L+0.8d)}

where v is the speed of sound, L is the length of the resonant tube, d is the diameter of the tube, f is the resonate sound frequency, and λ is the resonant wavelength.

Closed

A closed tube (also called a "stopped pipe" in the organ) is a tube which is closed at one end. The tube has a fundamental frequency but can be overblown to produce other higher frequencies or notes. These overblown registers can be tuned by using different degrees of conical taper. A closed tube resonates at the same fundamental frequency as an open tube twice its length, with a wavelength equal to four times its length. In a closed tube, a node, or point of no vibration, always appears at the closed end and if the tube is resonating, it will have an antinode, or point greatest vibration at the Phi point (length × 0.618) near the open end.

By overblowing a cylindrical closed tube, a note can be obtained that is approximately a twelfth above the fundamental note of the tube. This is sometimes described as one-fifth above the octave of the fundamental note. For example, if the fundamental note of a closed pipe is C1, then overblowing the pipe gives G2, which is one-twelfth above C1. Alternatively we can say that G2 is one-fifth above C2 — the octave above C1. Adjusting the taper of this cylinder for a decreasing cone can tune the second harmonic or overblown note close to the octave position or 8th. (ref: Horns,Strings and Harmony, by Arthur H. Benade.) Opening a small "speaker hole" at the Phi point, or shared "wave/node" position will cancel the fundamental frequency and force the tube to resonate at a 12th above the fundamental. This technique is used in a Recorder by pinching open the dorsal thumb hole. Moving this small hole upwards, closer to the voicing will make it an "Echo Hole" (Dolmetsch Recorder Modification) that will give a precise half note above the fundamental when opened. Note: Slight size or diameter adjustment is needed to zero in on the precise half note frequency.[5]

A closed tube will have approximate resonances of:

f = {nv \over 4L}

where "n" here is an odd number (1, 3, 5...). This type of tube produces only odd harmonics and has its fundamental frequency an octave lower than that of an open cylinder (that is, half the frequency).

A more accurate equation is given below:

f = {nv \over 4(L+0.4d)}.

Again, when n is 1:

f = {v \over 4(L+0.4d)}
{f(4(L+0.4d))} = v
{f\lambda} = v
\lambda = {4(L+0.4d)}

where v is the speed of sound, L is the length of the resonant tube, d is the diameter of the tube, f is the resonate sound frequency, and λ is the resonant wavelength.

Cones

An open conical tube, that is, one in the shape of a frustum of a cone with both ends open, will have resonant frequencies approximately equal to those of an open cylindrical pipe of the same length.

The resonant frequencies of a stopped conical tube — a complete cone or frustum with one end closed — satisfy a more complicated condition:

kL = n\pi - \tan^{-1} kx

where the wavenumber k is

k = 2\pi f/v

and x is the distance from the small end of the frustum to the vertex. When x is small, that is, when the cone is nearly complete, this becomes

k(L+x) \approx n\pi

leading to resonant frequencies approximately equal to those of an open cylinder whose length equals L + x. In words, a complete conical pipe behaves approximately like an open cylindrical pipe of the same length, and to first order the behavior does not change if the complete cone is replaced by a closed frustum of that cone.

Closed rectangular box

Sound waves in a rectangular box include such examples as loudspeaker enclosures and buildings. Rectangular building have resonances described as room modes. For a rectangular box, the resonant frequencies are given by[6]

f = {v \over 2} \sqrt{\left({\ell \over L_x}\right)^2 + \left({m \over L_y}\right)^2 + \left({n \over L_z}\right)^2}

where v is the speed of sound, Lx and Ly and Lz are the dimensions of the box. 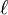\ell, n, and m are nonnegative integers that cannot all be zero. If the small loudspeaker box is airtight the frequency low enough and the compression is high enough, the sound pressure (decibel level) inside the box will be the same anywhere inside the box, this is hydraulic pressure.

Resonance of a sphere of air (vented)

The resonant frequency of an rigid cavity of static volume V0 with a necked sound hole of area A and length L is given by the Helmholtz resonance formula[7]

f = \frac{v}{2\pi}\sqrt{\frac{A}{V_0 L_{eq}}}

where L_{eq} is the equivalent length of the neck with end correction

L_{eq}= L+0.75d            for an unflanged neck[8]
L_{eq}= L+0.85d            for a flanged neck


For a spherical cavity, the resonant frequency formula becomes

f = \frac{vd}{\pi}\sqrt{\frac{3}{8L_{eq}D^3} }

where

D = diameter of sphere
d = diameter of sound hole


For a sphere with just a sound hole, L=0 and the surface of the sphere acts as a flange, so

f = \frac{v}{\pi}\sqrt{\frac{3d}{8(0.85)D^3} }

In dry air at 20°C, with d and D in metres, f in Hertz, this becomes

f = 72.6\sqrt{\frac{d}{D^3} }

False tones

Some large conical instruments like tubas have a strong and useful resonance that is not in the well-known harmonic series. For example, most large B♭ tubas have a strong resonance at low E♭ (E♭1, 39 Hz), which is between the fundamental and the second harmonic (an octave higher than the fundamental). These alternative resonances are often known as false tones or privileged tones.

The most convincing explanation for false-tones is that the horn is acting as a 'third of a pipe' rather than as a half-pipe. The bell remains an anti-node, but there would then be a node 1/3 of the way back to the mouthpiece. If so, it seems that the fundamental would be missing entirely, and would only be inferred from the overtones. However, the node and the anti-node collide in the same spot and cancel out the fundamental.

Resonance in musical composition

Several composers have begun to make resonance the subject of compositions. Alvin Lucier has used acoustic instruments and sine wave generators to explore the resonance of objects large and small in many of his compositions. The complex inharmonic partials of a swell shaped crescendo and decrescendo on a tamtam or other percussion instrument interact with room resonances in James Tenney's Koan: Having Never Written A Note For Percussion. Pauline Oliveros and Stuart Dempster regularly perform in large reverberant spaces such as the 2-million-US-gallon (7,600 m3) cistern at Fort Worden, WA, which has a reverb with a 45-second decay. Malmö Academy of Music composition professor and composer Kent Olofsson's "Terpsichord, a piece for percussion and pre-recorded sounds, [uses] the resonances from the acoustic instruments [to] form sonic bridges to the pre-recorded electronic sounds, that, in turn, prolong the resonances, re-shaping them into new sonic gestures." [9]

See also

External links

References

  1. ↑ Kinsler L.E., Frey A.R., Coppens A.B., Sanders J.V., "Fundamentals of Acoustics", 3rd Edition, ISBN 978-0-471-02933-5, Wiley, New York, 1982.
  2. ↑ Breaking Glass with Sound
  3. ↑ Tutorial on how to break glass with sound
  4. ↑ Wolfe, Joe. "Saxophone acoustics: an introduction". University of New South Wales. Retrieved 1 January 2015.
  5. 1 2 Kool, Jaap. Das Saxophon. J. J. Weber, Leipzig. 1931. Translated by Lawrence Gwozdz in 1987, discusses "open" and "closed" tubes.
  6. ↑ Kuttruff, Heinrich (2007). Acoustics: An Introduction. Taylor & Francis. p. 170. ISBN 978-0-203-97089-8.
  7. ↑ Wolfe, Joe. "Helmholtz Resonance". University of New South Wales. Retrieved 1 January 2015.
  8. ↑ Raichel, Daniel R. (2006). The Science and Applications of Acoustics. Springer. pp. 145–149. ISBN 978-0387-26062-4.
  9. ↑ Olofsson, Kent (4 February 2015). "Resonances and Responses". Divergence Press (University of Haddersfield Press) (4).
This article is issued from Wikipedia - version of the Thursday, February 04, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.