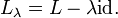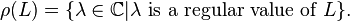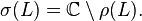Resolvent set

In linear algebra and operator theory, the resolvent set of a linear operator is a set of complex numbers for which the operator is in some sense "well-behaved". The resolvent set plays an important role in the resolvent formalism.

Definitions

Let X be a Banach space and let 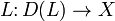$L\colon D(L)\rightarrow X$ be a linear operator with domain 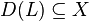$D(L) \subseteq X$ . Let id denote the identity operator on X. For any $\lambda \in \mathbb{C}$ , let

L_{\lambda} = L - \lambda \mathrm{id}.

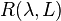$\lambda$ is said to be a regular value if $R(\lambda, L)$ , the inverse operator to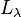 $L_\lambda$

exists, that is, 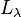$L_\lambda$ is injective;
is a bounded linear operator;
is defined on a dense subspace of X.

The resolvent set of L is the set of all regular values of L:

\rho (L) = \{ \lambda \in \mathbb{C} | \lambda \mbox{ is a regular value of } L \}.

The spectrum is the complement of the resolvent set:

\sigma (L) = \mathbb{C} \setminus \rho (L).

The spectrum can be further decomposed into the point/discrete spectrum (where condition 1 fails), the continuous spectrum (where conditions 1 and 3 hold but condition 2 fails) and the residual/compression spectrum (where condition 1 holds but condition 3 fails).

Properties

The resolvent set 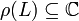$\rho(L) \subseteq \mathbb{C}$ of a bounded linear operator L is an open set.

References

Renardy, Michael; Rogers, Robert C. (2004). An introduction to partial differential equations. Texts in Applied Mathematics 13 (Second ed.). New York: Springer-Verlag. xiv+434. ISBN 0-387-00444-0. MR 2028503 (See section 8.3)

External links

Voitsekhovskii, M.I. (2001), "Resolvent set", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

Resolvent set

Definitions

Properties

References

External links

See also