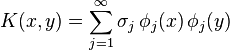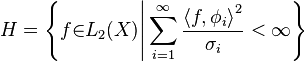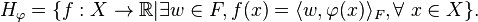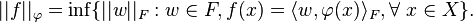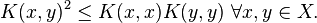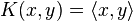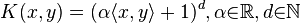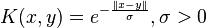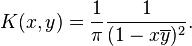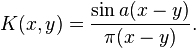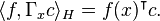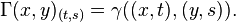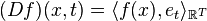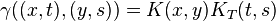Reproducing kernel Hilbert space
In functional analysis (a branch of mathematics), a reproducing kernel Hilbert space (RKHS) is a Hilbert space associated with a kernel that reproduces every function in the space in the sense that for any  in the set on which the functions are defined, "evaluation at
in the set on which the functions are defined, "evaluation at  " can be performed by taking an inner product with a function determined by the kernel. Such a reproducing kernel exists if and only if every evaluation functional is bounded.
" can be performed by taking an inner product with a function determined by the kernel. Such a reproducing kernel exists if and only if every evaluation functional is bounded.
The reproducing kernel was first introduced in the 1907 work of Stanisław Zaremba concerning boundary value problems for harmonic and biharmonic functions. James Mercer simultaneously examined functions which satisfy the reproducing property in the theory of integral equations. The idea of the reproducing kernel remained untouched for nearly twenty years until it appeared in the dissertations of Gábor Szegő, Stefan Bergman, and Salomon Bochner. The subject was eventually systematically developed in the early 1950s by Nachman Aronszajn and Stefan Bergman. [1]
These spaces have wide applications, including complex analysis, harmonic analysis, and quantum mechanics. Reproducing kernel Hilbert spaces are particularly important in the field of statistical learning theory because of the celebrated representer theorem which states that every function in an RKHS can be written as a linear combination of the kernel function evaluated at the training points. This is a practically useful result as it effectively simplifies the empirical risk minimization problem from an infinite dimensional to a finite dimensional optimization problem.
For ease of understanding, we provide the framework for real-valued Hilbert spaces. The theory can be easily extended to spaces of complex-valued functions and hence include the many important examples of reproducing kernel Hilbert spaces that are spaces of analytic functions. [2]
Definition
Let X be an arbitrary set and H a Hilbert space of real-valued functions on X. The evaluation functional over the Hilbert space of functions H is a linear functional that evaluates each function at a point x,
We say that H is a reproducing kernel Hilbert space if 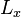 is continuous at any
is continuous at any  in
in  or, equivalently, if for all
or, equivalently, if for all  in X,
in X, 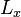 is a bounded operator on
is a bounded operator on  , i.e. there exists some M > 0 such that
, i.e. there exists some M > 0 such that
-
![L_{x}[f] := f(x) \le M \|f\|_H \text{ } \forall f \in H. \,](../I/m/df131f500ead2ed7fcda12b09d15e9d4.png)
(1)
While property (1) is the weakest condition that ensures both the existence of an inner product and the evaluation of every function in H at every point in the domain, it does not lend itself to easy application in practice. A more intuitive definition of the RKHS can be obtained by observing that this property guarantees that the evaluation functional can be represented by taking the inner product of  with a function
with a function 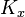 in H . This function is the so-called reproducing kernel for the Hilbert space H from which the RKHS takes its name. More formally, the Riesz representation theorem implies that for all x in X there exists a unique element
in H . This function is the so-called reproducing kernel for the Hilbert space H from which the RKHS takes its name. More formally, the Riesz representation theorem implies that for all x in X there exists a unique element 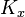 of H with the reproducing property,
of H with the reproducing property,
-
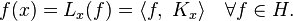
(2)
Since 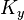 is itself a function in H we have that for each y in X
is itself a function in H we have that for each y in X
This allows us to define the reproducing kernel of H as a function 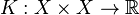 by
by
From this definition it is easy to see that 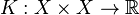 is both symmetric and positive definite, i.e.
is both symmetric and positive definite, i.e.
for any 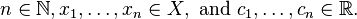 [3] The Moore-Aronszajn theorem (see below) is a sort of converse to this: if a function
[3] The Moore-Aronszajn theorem (see below) is a sort of converse to this: if a function  satisfies these conditions then there is a Hilbert space of functions on
satisfies these conditions then there is a Hilbert space of functions on  for which it is a reproducing kernel.
for which it is a reproducing kernel.
Example
The space of bandlimited functions  is a RKHS. Let
is a RKHS. Let
where 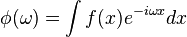 is the Fourier transform of
is the Fourier transform of  . One can show that if
. One can show that if  then
then
for some ![\phi \in L_2[-a,a]](../I/m/bf9fbbda3879241aca96c7f6438d00a2.png) . It then follows by the Cauchy-Schwarz inequality and Plancherel's Theorem that
. It then follows by the Cauchy-Schwarz inequality and Plancherel's Theorem that
As this inequality shows that the evaluation functional is bounded and  is also a Hilbert space,
is also a Hilbert space,  is indeed a RKHS.
is indeed a RKHS.
The kernel function 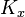 in this case is given by
in this case is given by
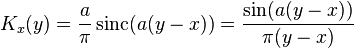 .
.
Note, that 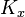 in this case is the "bandlimited version" of the Dirac delta distribution and that
in this case is the "bandlimited version" of the Dirac delta distribution and that 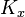 converges to
converges to  in the weak sense, as explained in the entry for the sinc function.
in the weak sense, as explained in the entry for the sinc function.
Moore–Aronszajn theorem
We have seen how a reproducing kernel Hilbert space defines a reproducing kernel function that is both symmetric and positive definite. The Moore-Aronszajn theorem goes in the other direction; it states that every symmetric, positive definite kernel defines a unique reproducing kernel Hilbert space. The theorem first appeared in Aronszajn's Theory of Reproducing Kernels, although he attributes it to E. H. Moore.
Theorem. Suppose K is a symmetric, positive definite kernel on a set X. Then there is a unique Hilbert space of functions on X for which K is a reproducing kernel.
Proof. For all x in X, define Kx = K(x, ⋅ ). Let H0 be the linear span of {Kx : x ∈ X}. Define an inner product on H0 by
The symmetry of this inner product follows from the symmetry of K and the non-degeneracy follows from the fact that K is positive definite.
Let H be the completion of H0 with respect to this inner product. Then H consists of functions of the form
where 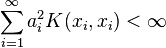 . The fact that the above sum converges for every x follows from the Cauchy-Schwarz inequality.
. The fact that the above sum converges for every x follows from the Cauchy-Schwarz inequality.
Now we can check the reproducing property (2):
To prove uniqueness, let G be another Hilbert space of functions for which K is a reproducing kernel. For any x and y in X, (2) implies that
By linearity,  on the span of {Kx : x ∈ X}. Then G = H by the uniqueness of the completion.
on the span of {Kx : x ∈ X}. Then G = H by the uniqueness of the completion.
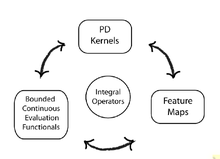
Integral operators and Mercer's theorem
We may characterize a symmetric positive definite kernel  via the integral operator using Mercer's theorem and obtain an additional view of the RKHS. Let
via the integral operator using Mercer's theorem and obtain an additional view of the RKHS. Let  be a compact space equipped with a strictly positive finite Borel measure
be a compact space equipped with a strictly positive finite Borel measure  and
and 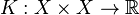 a continuous, symmetric, and positive definite function. Define the integral operator
a continuous, symmetric, and positive definite function. Define the integral operator 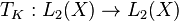 as
as
where 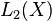 is the space of square integrable functions with respect to
is the space of square integrable functions with respect to  .
.
Mercer's theorem states that the spectral decomposition of the integral operator 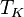 of
of  yields a series representation of
yields a series representation of  in terms of the eigenvalues and eigenfunctions of
in terms of the eigenvalues and eigenfunctions of 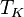 . This then implies that
. This then implies that  is a reproducing kernel so that the corresponding RKHS can be defined in terms of these eigenvalues and eigenfunctions. We provide the details below.
is a reproducing kernel so that the corresponding RKHS can be defined in terms of these eigenvalues and eigenfunctions. We provide the details below.
Under these assumptions 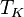 is a compact, continuous, self-adjoint, and positive operator. The spectral theorem for self-adjoint operators implies that there is an at most countable decreasing sequence
is a compact, continuous, self-adjoint, and positive operator. The spectral theorem for self-adjoint operators implies that there is an at most countable decreasing sequence 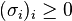 such that
such that 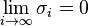 and
and
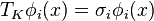 , where the
, where the 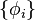 form an orthonormal basis of
form an orthonormal basis of 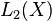 . By the positivity
. By the positivity 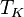 ,
, 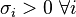 . One can also show that
. One can also show that 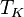 maps continuously into the space of continuous functions
maps continuously into the space of continuous functions 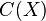 and therefore we may choose continuous functions as the eigenvectors, that is,
and therefore we may choose continuous functions as the eigenvectors, that is, 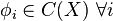 . Then by Mercer's theorem
. Then by Mercer's theorem
 may be written in terms of the eigenvalues and continuous eigenfunctions as
may be written in terms of the eigenvalues and continuous eigenfunctions as
for all  in
in  such that
such that 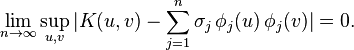 This above series representation is referred to as a Mercer kernel or Mercer representation of
This above series representation is referred to as a Mercer kernel or Mercer representation of  .
.
Furthermore, it can be shown that the RKHS  of
of  is given by
is given by
where the inner product of  given by
given by 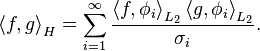 This representation of the RKHS has application in probability and statistics, for example to the Karhunen-Loeve representation for stochastic processes and kernel PCA.
This representation of the RKHS has application in probability and statistics, for example to the Karhunen-Loeve representation for stochastic processes and kernel PCA.
Feature maps
A feature map is a map  , where
, where  is a Hilbert space which we will call the feature space. The first sections presented the connection between bounded/continuous evaluation functions, positive definite functions, and integral operators and in this section we provide another representation of the RKHS in terms of feature maps.
is a Hilbert space which we will call the feature space. The first sections presented the connection between bounded/continuous evaluation functions, positive definite functions, and integral operators and in this section we provide another representation of the RKHS in terms of feature maps.
We first note that every feature map defines a kernel via
-
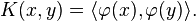
(3)
Clearly  is symmetric and positive definiteness follows from the properties of inner product in
is symmetric and positive definiteness follows from the properties of inner product in  . Conversely, every positive definite function and corresponding reproducing kernel Hilbert space has infinitely many associated feature maps such that (3) holds.
. Conversely, every positive definite function and corresponding reproducing kernel Hilbert space has infinitely many associated feature maps such that (3) holds.
For example, we can trivially take 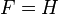 and
and 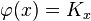 for all
for all  . Then (3) is satisfied by the reproducing property. Another classical example of a feature map relates to the previous section regarding integral operators by taking
. Then (3) is satisfied by the reproducing property. Another classical example of a feature map relates to the previous section regarding integral operators by taking 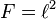 and
and 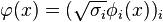 .
.
This connection between kernels and feature maps provides us with a new way to understand positive definite functions and hence reproducing kernels as inner products in  . Moreover, every feature map can naturally define a RKHS by means of the definition of a positive definite function.
. Moreover, every feature map can naturally define a RKHS by means of the definition of a positive definite function.
Lastly, feature maps allow us to construct function spaces that reveal another perspective on the RKHS. Consider the linear space
We can define a norm on 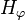 by
by
It can be shown that 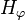 is a RKHS with kernel defined by
is a RKHS with kernel defined by 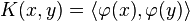 . This representation implies that the elements of the RKHS are inner products of elements in the feature space and can accordingly be seen as hyperplanes. This view of the RKHS is related to the kernel trick in machine learning. [4]
. This representation implies that the elements of the RKHS are inner products of elements in the feature space and can accordingly be seen as hyperplanes. This view of the RKHS is related to the kernel trick in machine learning. [4]
Properties
The following properties of RKHSs may be useful to readers.
- Let
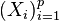 be a sequence of sets and
be a sequence of sets and 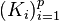 be a collection of corresponding positive definite functions on
be a collection of corresponding positive definite functions on 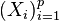 . It then follows that
. It then follows that
is a kernel on 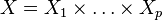 .
.
- Let
 , then the restriction of
, then the restriction of  to
to 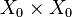 is also a reproducing kernel.
is also a reproducing kernel.
- Consider a normalized kernel
 such that
such that 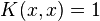 for all
for all  . Define a pseudo-metric on X as
. Define a pseudo-metric on X as
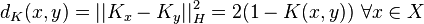 .
.
By the Cauchy–Schwarz inequality,
This inequality allows us to view  as a measure of similarity between inputs. If
as a measure of similarity between inputs. If  are similar then
are similar then 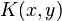 will be closer to 1 while if
will be closer to 1 while if  are dissimilar then
are dissimilar then 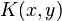 will be closer to 0.
will be closer to 0.
- The closure of the span of
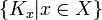 coincides with
coincides with  . [5]
. [5]
Examples
Common examples of kernels include:
- Linear Kernel:
- Polynomial Kernel:
Other common examples are kernels which satisfy 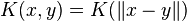 . These are the radial basis function kernels.
. These are the radial basis function kernels.
- Radial Basis Function Kernels:
- Gaussian Kernel:
- Sometimes referred to as the Radial basis function kernel, or squared exponential kernel
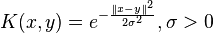
- Laplacian Kernel:
We also provide examples of Bergman kernels. Let X be finite and let H consist of all complex-valued functions on X. Then an element of H can be represented as an array of complex numbers. If the usual inner product is used, then Kx is the function whose value is 1 at x and 0 everywhere else, and K(x,y) can be thought of as an identity matrix since K(x,y)=1 when x=y and K(x,y)=0 otherwise. In this case, H is isomorphic to Cn.
The case of X = D (where D denotes the unit disc) is more sophisticated. Here the Bergman space H2(D) is the space of square-integrable holomorphic functions on D. It can be shown that the reproducing kernel for H2(D) is
Lastly, the space of band limited functions  in
in  with bandwidth
with bandwidth  are a RKHS with reproducing kernel
are a RKHS with reproducing kernel
Extension to vector-valued functions
In this section we extend the definition of the RKHS to spaces of vector-valued functions as this extension is particularly important in multi-task learning and manifold regularization. The main difference is that the reproducing kernel  is a symmetric function that is now a positive semi-definite matrix for any
is a symmetric function that is now a positive semi-definite matrix for any  in
in  . More formally, we define a vector-valued RKHS (vvRKHS) as a Hilbert space of functions
. More formally, we define a vector-valued RKHS (vvRKHS) as a Hilbert space of functions 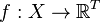 such that for all
such that for all  and
and 
and
This second property parallels the reproducing property for the scalar-valued case. We note that this definition can also be connected to integral operators, bounded evaluation functions, and feature maps as we saw for the scalar-valued RKHS. We can equivalently define the vvRKHS as a vector-valued Hilbert space with a bounded evaluation functional and show that this implies the existence of a unique reproducing kernel by the Riesz Representation theorem. Mercer's theorem can also be extended to address the vector-valued setting and we can therefore obtain a feature map view of the vvRKHS. Lastly, it can also be shown that the closure of the span of 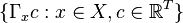 coincides with
coincides with  , another property similar to the scalar-valued case.
, another property similar to the scalar-valued case.
We can gain intuition for the vvRKHS by taking a component-wise perspective on these spaces. In particular, we find that every vvRKHS is isometrically isomorphic to a scalar-valued RKHS on a particular input space. Let 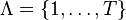 . Consider the space
. Consider the space 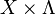 and the corresponding reproducing kernel
and the corresponding reproducing kernel
-
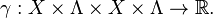
(4)
As noted above, the RKHS associated to this reproducing kernel is given by the closure of the span of 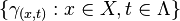 where
where
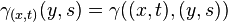 for every set of pairs
for every set of pairs 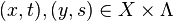 .
.
The connection to the scalar-valued RKHS can then be made by the fact that every matrix-valued kernel can be identified with a kernel of the form of (4) via
Moreover, every kernel with the form of (4) defines a matrix-valued kernel with the above expression. Now letting the map 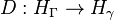 be defined as
be defined as
where 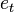 is the
is the 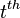 component of the canonical basis for
component of the canonical basis for  , one can show that
, one can show that  is bijective and an isometry between
is bijective and an isometry between 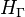 and
and 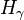 .
.
While this view of the vvRKHS can be quite useful in multi-task learning, it should be noted that this isometry does not reduce the study of the vector-valued case to that of the scalar-valued case. In fact, this isometry procedure can make both the scalar-valued kernel and the input space too difficult to work with in practice as properties of the original kernels are often lost. [6] [7] [8]
An important class of matrix-valued reproducing kernels are separable kernels which can factorized as the product of a scalar valued kernel and a  -dimensional symmetric positive semi-definite matrix. In light of our previous discussion these kernels are of the form
-dimensional symmetric positive semi-definite matrix. In light of our previous discussion these kernels are of the form
for all  in
in  and
and  in
in  . As the scalar-valued kernel encodes dependencies between the inputs, we can observe that the matrix-valued kernel encodes dependencies among both the inputs and the outputs.
. As the scalar-valued kernel encodes dependencies between the inputs, we can observe that the matrix-valued kernel encodes dependencies among both the inputs and the outputs.
We lastly remark that the above theory can be further extended to spaces of functions with values in function spaces but obtaining kernels for these spaces is a more difficult task. [9]
See also
- Positive definite kernel
- Mercer's theorem
- Kernel trick
- Kernel embedding of distributions
- Representer theorem
Notes
References
- Alvarez, Mauricio, Rosasco, Lorenzo and Lawrence, Neil, “Kernels for Vector-Valued Functions: a Review,” http://arxiv.org/abs/1106.6251, June 2011.
- Aronszajn, Nachman (1950). "Theory of Reproducing Kernels". Transactions of the American Mathematical Society 68 (3): 337–404. doi:10.1090/S0002-9947-1950-0051437-7. JSTOR 1990404. MR 51437.
- Berlinet, Alain and Thomas, Christine. Reproducing kernel Hilbert spaces in Probability and Statistics, Kluwer Academic Publishers, 2004.
- Cucker, Felipe; Smale, Steve (2002). "On the Mathematical Foundations of Learning". Bulletin of the American Mathematical Society 39 (1): 1–49. doi:10.1090/S0273-0979-01-00923-5. MR 1864085.
- De Vito, Ernest, Umanita, Veronica, and Villa, Silvia. "An extension of Mercer theorem to vector-valued measurable kernels," http://arxiv.org/pdf/1110.4017.pdf, June 2013.
- Durrett, Greg. 9.520 Course Notes, Massachusetts Institute of Technology, http://www.mit.edu/~9.520/scribe-notes/class03_gdurett.pdf, February 2010.
- Kimeldorf, George; Wahba, Grace (1971). "Some results on Tchebycheffian Spline Functions" (PDF). Journal of Mathematical Analysis and Applications 33 (1): 82–95. doi:10.1016/0022-247X(71)90184-3. MR 290013.
- Okutmustur, Baver. “Reproducing Kernel Hilbert Spaces,” Ph.D. dissertation, Bilkent University, http://www.thesis.bilkent.edu.tr/0002953.pdf, August 2005.
- Paulsen, Vern. “An introduction to the theory of reproducing kernel Hilbert spaces,” http://www.math.uh.edu/~vern/rkhs.pdf.
- Steinwart, Ingo; Scovel, Clint (2012). "Mercer’s theorem on general domains: On the interaction between measures, kernels, and RKHSs". Consty. Approx. 35 (3): 363–417. MR 2914365.
- Rosasco, Lorenzo and Poggio, Thomas. "A Regularization Tour of Machine Learning - MIT 9.520 Lecture Notes" Manuscript, Dec. 2014.
- Wahba, Grace, Spline Models for Observational Data, SIAM, 1990.
- Zhang, Haizhang, Xu, Yuesheng, and Zhang, Qinghui (2012). "Refinement of Operator-valued Reproducing Kernels." Journal of Machine Learning Research 13 91-136.
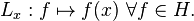
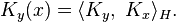
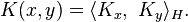
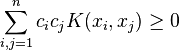
![H = \{ f \in L_2(\mathbb{R}) | \operatorname{supp}(\phi) \subset [-a,a], a < \infty \}](../I/m/6ed7a790a3be47bf173666de9df8aeaa.png)
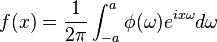
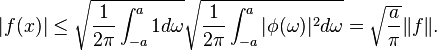
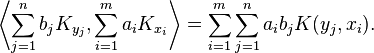
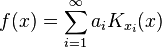

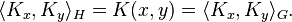
 =\int_X K(\cdot,t) f(t)\, d\mu(t)](../I/m/5f9cca09fd850bf900c199fb2a5ed1bd.png)