Renormalon

In physics, a renormalon (a term suggested by 't Hooft[1]) is a particular source of divergence seen in perturbative approximations to quantum field theories (QFT). When a formally divergent series in a QFT is summed using Borel summation, the associated Borel transform of the series can have singularities as a function of the complex transform parameter.[2] The renormalon is a possible type of singularity arising in this complex Borel plane, and is a counterpart of an instanton singularity. 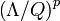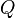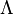Associated with such singularities, renormalon contributions are discussed in the context of quantum chromodynamics (QCD)[2] and usually have the power-like form \left(\Lambda/Q\right)^p as functions of the momentum Q (here \Lambda is the momentum cut-off). 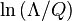They are cited against the usual logarithmic effects like \ln\left(\Lambda/Q\right).

Brief history

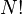Perturbation series in quantum field theory are usually divergent as was firstly indicated by Freeman Dyson.[3] According to the Lipatov method,[4] N-th order contribution of perturbation theory into any quantity can be evaluated at large N in the saddle-point approximation for functional integrals and is determined by instanton configurations. This contribution behaves usually as N! in dependence on N and is frequently associated with approximately the same (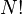N!) number of Feynman diagrams. Lautrup[5] has noted that there exist individual diagrams giving approximately the same contribution. In principle, it is possible that such diagrams are automatically taken into account in Lipatov’s calculation, because its interpretation in terms of diagrammatic technique is problematic. However, 't Hooft put forward a conjecture that Lipatov's and Lautrup's contributions are related with different types of singularities in the Borel plane, the former with instanton ones and the latter with renormalon ones. Existence of instanton singularities is beyond any doubt, while existence of renormalon ones was never proved rigorously in spite of numerous efforts. Among the essential contributions one should mention the application of the operator product expansion, as was suggested by Parisi.[6]

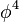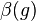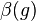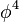Recently a proof was suggested for absence of renormalon singularities in \phi^4 theory and a general criterion for their existence was formulated[7] in terms of the asymptotic behavior of the Gell-Mann - Low function \beta(g). Analytical results for asymptotics of \beta(g) in \phi^4 theory[8] and QED[9] indicate the absence of renormalon singularities in these theories.

References

  1. ↑ 't Hooft G, in: The whys of subnuclear physics (Erice, 1977), ed. A Zichichi, Plenum Press, New York, 1979.
  2. 1 2 Beneke, M. (August 1999). "Renormalons". Physics Reports 37 (1-2): 1–142. arXiv:hep-ph/9807443. Bibcode:1999PhR...317....1B. doi:10.1016/S0370-1573(98)00130-6. Retrieved 20 April 2013.
  3. ↑ F.J.Dyson, Phys.Rev. 85, 631 (1952)
  4. ↑ L.N.Lipatov, Zh.Eksp.Teor.Fiz. 72, 411(1977) [Sov.Phys. JETP 45, 216 (1977)].
  5. ↑ B.Lautrup, Phys.Lett. B 69, 109 (1977).
  6. ↑ G.Parisi, Phys.Lett. B 76, 65 (1978); Nucl.Phys. B 150, 163 (1979).
  7. ↑ I. M. Suslov, JETP 100, 1188 (2005), http://arxiv.org/abs/hep-ph/0510142.
  8. ↑ I. M. Suslov, JETP 107, 413 (2008), http://arxiv.org/abs/1010.4081; JETP 111, 450 (2010), http://arxiv.org/abs/1010.4317.
  9. ↑ I. M. Suslov, JETP 108, 980 (2009), http://arxiv.org/abs/0804.2650.
This article is issued from Wikipedia - version of the Sunday, August 24, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.