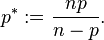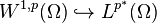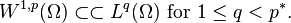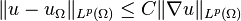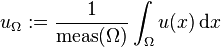Rellich–Kondrachov theorem

In mathematics, the Rellich–Kondrachov theorem is a compact embedding theorem concerning Sobolev spaces. It is named after the Italian-Austrian mathematician Franz Rellich and the Russian mathematician Vladimir Iosifovich Kondrashov. Rellich proved the L² theorem and Kondrachov the L^p theorem.

Statement of the theorem

Let Ω ⊆ Rⁿ be an open, bounded Lipschitz domain, and let 1 ≤ p < n. Set

p^{*} := \frac{n p}{n - p}.

Then the Sobolev space W^1,p(Ω; R) is continuously embedded in the L^p space L^{p^∗}(Ω; R) and is compactly embedded in L^q(Ω; R) for every 1 ≤ q < p^∗. In symbols,

W^{1, p} (\Omega) \hookrightarrow L^{p^{*}} (\Omega)

and

W^{1, p} (\Omega) \subset \subset L^{q} (\Omega) \mbox{ for } 1 \leq q < p^{*}.

Kondrachov embedding theorem

On a compact manifold with $C 1$ boundary, the Kondrachov embedding theorem states that if $k > ℓ$ and $k - n / p > ℓ - n / q$ then the Sobolev embedding

W^{k,p}(M)\subset W^{\ell,q}(M)

is completely continuous (compact).

Consequences

Since an embedding is compact if and only if the inclusion (identity) operator is a compact operator, the Rellich–Kondrachov theorem implies that any uniformly bounded sequence in W^1,p(Ω; R) has a subsequence that converges in L^q(Ω; R). Stated in this form, in the past the result was sometimes referred to as the Rellich-Kondrachov selection theorem, since one "selects" a convergent subsequence. (However, today the customary name is "compactness theorem", whereas "selection theorem" has a precise and quite different meaning, referring to multifunctions).

The Rellich–Kondrachov theorem may be used to prove the Poincaré inequality,^[1] which states that for u ∈ W^1,p(Ω; R) (where Ω satisfies the same hypotheses as above),

\| u - u_{\Omega} \|_{L^{p} (\Omega)} \leq C \| \nabla u \|_{L^{p} (\Omega)}

for some constant C depending only on p and the geometry of the domain Ω, where

u_{\Omega} := \frac{1}{\mathrm{meas} (\Omega)} \int_{\Omega} u(x) \, \mathrm{d} x

denotes the mean value of u over Ω.

References

↑ Evans, Lawrence C. (2010). "§5.8.1". Partial Differential Equations (2nd ed.). p. 290. ISBN 0-8218-4974-3.

Literature

Evans, Lawrence C. (2010). Partial Differential Equations (2nd ed.). American Mathematical Society. ISBN 0-8218-4974-3.

Rellich, Franz (24 January 1930). "Ein Satz über mittlere Konvergenz". Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (in German) 1930: 30–35. Zbl 56.0224.02.

This article is issued from Wikipedia - version of the Friday, October 16, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.