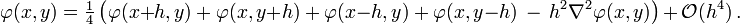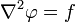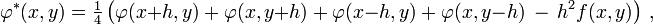Relaxation (iterative method)

This article is about iterative methods for solving systems of equations. For other uses, see Relaxation (disambiguation).

In numerical mathematics, relaxation methods are iterative methods for solving systems of equations, including nonlinear systems.[1]

Relaxation methods were developed for solving large sparse linear systems, which arose as finite-difference discretizations of differential equations.[2][3] They are also used for the solution of linear equations for linear least-squares problems[4] and also for systems of linear inequalities, such as those arising in linear programming.[5][6][7] They have also been developed for solving nonlinear systems of equations.[1]

Relaxation methods are important especially in the solution of linear systems used to model elliptic partial differential equations, such as Laplace's equation and its generalization, Poisson's equation. These equations describe boundary-value problems, in which the solution-function's values are specified on boundary of a domain; the problem is to compute a solution also on its interior. Relaxation methods are used to solve the linear equations resulting from a discretization of the differential equation, for example by finite differences.[4][3][2]

These iterative methods of relaxation should not be confused with "relaxations" in mathematical optimization, which approximate a difficult problem by a simpler problem, whose "relaxed" solution provides information about the solution of the original problem.[7]

Synonyms

Iterative relaxation of solutions is commonly dubbed smoothing because relaxation of certain equations (such as Laplace's equation) resembles repeated application of a local smoothing filter to the solution vector.
Another name is stationary linear iterative method.

Model problem of potential theory

When φ is a smooth real-valued function on the real numbers, its second derivative can be approximated by:

\frac{d^2\varphi(x)}{{dx}^2} = \frac{\varphi(x{-}h)-2\varphi(x)+\varphi(x{+}h)}{h^2}\,+\,\mathcal{O}(h^2)\,.

Using this in both dimensions for a function φ of two arguments at the point (x, y), and solving for φ(x, y), results in:

\varphi(x, y) = \tfrac{1}{4}\left(\varphi(x{+}h,y)+\varphi(x,y{+}h)+\varphi(x{-}h,y)+\varphi(x,y{-}h) \,-\,h^2{\nabla}^2\varphi(x,y)\right)\,+\,\mathcal{O}(h^4)\,.

To approximate the solution of the Poisson equation:

{\nabla}^2 \varphi = f\,

numerically on a two-dimensional grid with grid spacing h, the relaxation method assigns the given values of function φ to the grid points near the boundary and arbitrary values to the interior grid points, and then repeatedly performs the assignment φ := φ* on the interior points, where φ* is defined by:

\varphi^*(x, y) = \tfrac{1}{4}\left(\varphi(x{+}h,y)+\varphi(x,y{+}h)+\varphi(x{-}h,y)+\varphi(x,y{-}h) \,-\,h^2f(x,y)\right)\,,

until convergence.[3][2]

The method, sketched here for two dimensions,[3][2] is readily generalized to other numbers of dimensions.

Convergence and acceleration

While the method converges under general conditions, it typically makes slower progress than competing methods. Nonetheless, the study of relaxation methods remains a core part of linear algebra, because the transformations of relaxation theory provide excellent preconditioners for new methods. Indeed, the choice of preconditioner is often more important than the choice of iterative method, according to Yousef Saad.[8]

Multigrid methods may be used to accelerate the methods. One can first compute an approximation on a coarser grid – usually the double spacing 2h – and use that solution with interpolated values for the other grid points as the initial assignment. This can then also be done recursively for the coarser computation.[8][9]

See also

Notes

  1. 1 2 Ortega, J. M.; Rheinboldt, W. C. (2000). Iterative solution of nonlinear equations in several variables. Classics in Applied Mathematics 30 (Reprint of the 1970 Academic Press ed.). Philadelphia, PA: Society for Industrial and Applied Mathematics (SIAM). pp. xxvi+572. ISBN 0-89871-461-3. MR 1744713.
  2. 1 2 3 4 Richard S. Varga 2002 Matrix Iterative Analysis, Second ed. (of 1962 Prentice Hall edition), Springer-Verlag.
  3. 1 2 3 4 David M. Young, Jr. Iterative Solution of Large Linear Systems, Academic Press, 1971. (reprinted by Dover, 2003)
  4. 1 2 Abraham Berman, Robert J. Plemmons, Nonnegative Matrices in the Mathematical Sciences, 1994, SIAM. ISBN 0-89871-321-8.
  5. ↑ Murty, Katta G. (1983). "16 Iterative methods for linear inequalities and linear programs (especially 16.2 Relaxation methods, and 16.4 Sparsity-preserving iterative SOR algorithms for linear programming)". Linear programming. New York: John Wiley & Sons Inc. pp. 453–464. ISBN 0-471-09725-X. MR 720547.
  6. ↑ Goffin, J.-L. (1980). "The relaxation method for solving systems of linear inequalities". Math. Oper. Res. 5 (3): 388–414. doi:10.1287/moor.5.3.388. JSTOR 3689446. MR 594854.
  7. 1 2 Minoux, M. (1986). Mathematical programming: Theory and algorithms. Egon Balas (foreword) (Translated by Steven Vajda from the (1983 Paris: Dunod) French ed.). Chichester: A Wiley-Interscience Publication. John Wiley & Sons, Ltd. pp. xxviii+489. ISBN 0-471-90170-9. MR 868279. (2008 Second ed., in French: Programmation mathématique: Théorie et algorithmes. Editions Tec & Doc, Paris, 2008. xxx+711 pp. ISBN 978-2-7430-1000-3. MR 2571910).
  8. 1 2 Yousef Saad, Iterative Methods for Sparse Linear Systems, 1st edition, PWS, 1996.
  9. ↑ William L. Briggs, Van Emden Henson, and Steve F. McCormick (2000), A Multigrid Tutorial (2nd ed.), Philadelphia: Society for Industrial and Applied Mathematics, ISBN 0-89871-462-1.

References

Further reading

This article is issued from Wikipedia - version of the Wednesday, June 03, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.