Reinhardt cardinal
In mathematical set theory, a Reinhardt cardinal is a large cardinal κ, suggested by William Nelson Reinhardt (1967, 1974).
Definition
A Reinhardt cardinal is the critical point of a non-trivial elementary embedding j of V into itself.
A minor technical problem is that this property cannot be formulated in the usual set theory ZFC: the embedding j is a class, which in ZFC means something of the form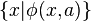 
for some set a and formula φ, but in the language of set theory it is not possible to quantify over all classes or define the truth of formulas. There are several ways to get round this. One way is to add a new function symbol j to the language of ZFC, together with axioms stating that j is an elementary embedding of V (and of course adding separation and replacement axioms for formulas involving j). Another way is to use a class theory such as NBG or KM. A third way would be to treat Kunen's theorem as a countable infinite collection of theorems, one for each formula φ, but that would trivialize the theorem. (It is possible to have nontrivial elementary embeddings of transitive models of ZFC into themselves assuming a mild large cardinal hypothesis, but these elementary embeddings are not classes of the model.)
Kunen's theorem
Kunen (1971) proved Kunen's inconsistency theorem showing that the existence of such an embedding contradicts NBG with the axiom of choice (and ZFC extended by j), but it is consistent with weaker class theories. His proof uses the axiom of choice, and it is still an open question as to whether such an embedding is consistent with NBG without the axiom of choice (or with ZF plus the extra symbol j and its attendant axioms).
Stronger cardinal axioms
There are some variations of Reinhardt cardinals.
In ZF, there is a hierarchy of hypotheses asserting existence of elementary embeddings V→V
J3: There is a nontrivial elementary embedding j: V→V
J2: There is a nontrivial elementary embedding j: V→V, and DCλ holds, where λ is the least fixed-point above the critical point.
J1: There is a cardinal κ such that for every α, there is an elementary embedding j : V→V with j(κ)>α and cp(j) = κ.
J2 implies J3, and J1 implies J3 and also implies consistency of J2. By adding a generic well-ordering of V to a model of J1, one gets ZFC plus a nontrivial elementary embedding of HOD into itself.
Berkeley cardinals are a stronger large cardinals suggested by Woodin.
References
- Jensen, Ronald (1995), "Inner Models and Large Cardinals", The Bulletin of Symbolic Logic (The Bulletin of Symbolic Logic, Vol. 1, No. 4) 1 (4): 393–407., doi:10.2307/421129, JSTOR 421129
- Kanamori, Akihiro (2003), The Higher Infinite : Large Cardinals in Set Theory from Their Beginnings (2nd ed.), Springer, ISBN 3-540-00384-3
- Kunen, Kenneth (1971), "Elementary embeddings and infinitary combinatorics", J. Symbolic Logic (The Journal of Symbolic Logic, Vol. 36, No. 3) 36 (3): 407–413, doi:10.2307/2269948, JSTOR 2269948, MR 0311478
- Reinhardt, W. N. (1967), Topics in the metamathematics of set theory, Doctoral dissertation, University of California, Berkeley
- Reinhardt, W. N. (1974), "Remarks on reflection principles, large cardinals, and elementary embeddings.", Axiomatic set theory, Proc. Sympos. Pure Math., XIII, Part II, Providence, R. I.: Amer. Math. Soc., pp. 189–205, MR 0401475
External links
- Koellner, Peter (2014), The Search for Deep Inconsistency (PDF)