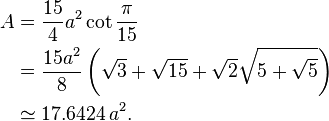Pentadecagon
| Regular pentadecagon | |
|---|---|
|
A regular pentadecagon | |
| Type | Regular polygon |
| Edges and vertices | 15 |
| Schläfli symbol | {15} |
| Coxeter diagram |
|
| Symmetry group | Dihedral (D15), order 2×15 |
| Internal angle (degrees) | 156° |
| Dual polygon | self |
| Properties | convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, a pentadecagon (or pentakaidecagon) is a fifteen-sided polygon or 15-gon.
Regular pentadecagon
A regular pentadecagon is represented by Schläfli symbol {15}.
A regular pentadecagon has interior angles of 156°, and with a side length a, has an area given by
Uses

A regular triangle, decagon, and pentadecagon can completely fill a plane vertex.
Construction
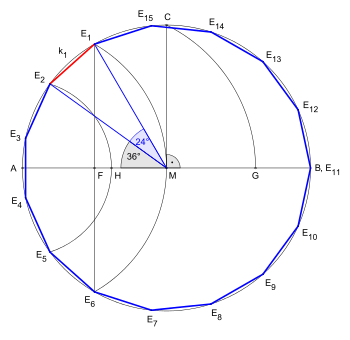
As 15 = 3 × 5, a regular pentadecagon is constructible using compass and straightedge: The following constructions of regular pentadecagons with given circumcircle are similar to the illustration of the proposition XVI in Book IV of Euclid's Elements.[1]
Comparison the construction according Euclid in this image: Pentadecagon
In the construction for given circumcircle: 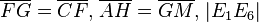 is a side of equilateral triangle and
is a side of equilateral triangle and 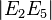 is a side of a regular pentagon.[2]
The point
is a side of a regular pentagon.[2]
The point  divides the radius
divides the radius 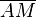 in golden ratio:
in golden ratio: 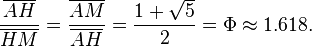
Compared with the first animation (with green lines) are in the following two images the two circular arcs (for angles 36° and 24°) rotated 90° counterclockwise shown. They do not use the segment 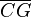 , but rather they use segment
, but rather they use segment 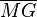 as radius
as radius 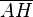 for the second circular arc (angle 36°).
for the second circular arc (angle 36°).


A compass and straightedge construction for a given side length. The construction is nearly equal to that of the pentagon at a given side, then also the presentation is succeed by extension one side and it generates a segment, here 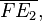 which is divided according to the golden ratio.
which is divided according to the golden ratio.

Circumradius 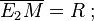 Side
Side 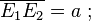 Angle
Angle 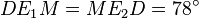
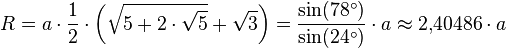
See also Calculation of the circumradius (German)


Symmetry

The regular pentadecagon has Dih15 dihedral symmetry, order 30, represented by 15 lines of reflection. Dih15 has 3 dihedral subgroups: Dih5, Dih3, and Dih1. And four more cyclic symmetries: Z15, Z5, Z3, and Z1, with Zn representing π/n radian rotational symmetry.
On the pentadecagon, there are 8 distinct symmetries. John Conway labels these symmetries with a letter and order of the symmetry follows the letter.[3] He gives r30 for the full reflective symmetry, Dih15. He gives d (diagonal) with reflection lines through vertices, p with reflection lines through edges (perpendicular), and for the odd-sided pentadecagon i with mirror lines through both vertices and edges, and g for cyclic symmetry. a1 labels no symmetry.
These lower symmetries allows degrees of freedoms in defining irregular pentadecagons. Only the g15 subgroup has no degrees of freedom but can seen as directed edges.
Pentadecagrams
There are 3 regular star polygons: {15/2}, {15/4}, {15/7}, constructed from the same 15 vertices of a regular pentadecagon, but connected by skipping every second, fourth, or seventh vertex respectively.
There are also three regular star figures: {15/3}, {15/5}, {15/6}, the first being a compound of 3 pentagons, the second a compound of 5 equilateral triangles, and the third is a compound of 3 pentagrams.
| Picture |  {15/2} |
.svg.png) {15/3} or 3{5} |
 {15/4} |
.svg.png) {15/5} or 5{3} |
.svg.png) {15/6} or 3{5/2} |
 {15/7} |
|---|---|---|---|---|---|---|
| Interior angle | 132° | 108° | 84° | 60° | 36° | 12° |
Petrie polygons
The regular pentadecagon is the Petrie polygon for some higher-dimensional polytopes, projected in a skew orthogonal projection:
 14-simplex (14D) |
It is also the Petrie polygon for the great 120-cell and grand stellated 120-cell.
References
- ↑ (English) Dunham, William (1991). Journey through Genius - The Great Theorems of Mathematics (PDF). Penguin. p. 65. Retrieved 2015-11-12 – via the University of Kentucky College of Arts & Sciences Mathematics.
- ↑ (German) Kepler, Johannes, translated and initiated by MAX CASPAR 1939. WELT-HARMONIK. München: R. OLDENBURG VERLAG 2006. p. 44. Retrieved 2015-12-07 – via Google Books. From the webarchive generated on 29 January 2016
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
External links
| ||||||||||||||||||||||||||