Reflexive sheaf

In algebraic geometry, a reflexive sheaf is a coherent sheaf that is isomorphic to its second dual (as a sheaf of modules) via the canonical map. The second dual of a coherent sheaf is called the reflexive hull of the sheaf. A basic example of a reflexive sheaf is a locally free sheaf and, in practice, a reflexive sheaf is thought of as a kind of a vector bundle modulo some singularity. The notion is important both in scheme theory and complex algebraic geometry.

A reflexive sheaf is torsion-free. The dual of a coherent sheaf is reflexive.[1] Usually, the product of reflexive sheaves is defined as the reflexive hull of their tensor products (so the result is reflexive.)

A coherent sheaf F is said to be "normal" in the sense of Barth if the restriction 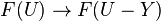F(U) \to F(U - Y) is bijective for every open subset U and a closed subset Y of U of codimension at least 2. With this terminology, a coherent sheaf on an integral normal scheme is reflexive if and only if it is torsion-free and normal in the sense of Barth.[2] A reflexive sheaf of rank one on an integral locally factorial scheme is invertible.[3]

A divisorial sheaf on a scheme X is a rank-one reflexive sheaf that is locally free at the generic points of the conductor DX of X.[4]

See also

Notes

  1. ↑ Hartshorne 1980, Corollary 1.2.
  2. ↑ Hartshorne 1980, Proposition 1.6.
  3. ↑ Hartshorne 1980, Proposition 1.9.
  4. ↑ Kollár, Ch. 3, § 1.

References

Further reading

External links

This article is issued from Wikipedia - version of the Thursday, September 10, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.