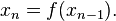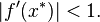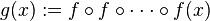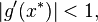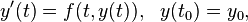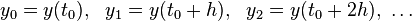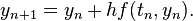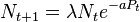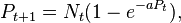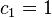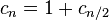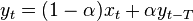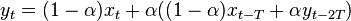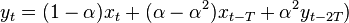Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence or multidimensional array of values, once one or more initial terms are given: each further term of the sequence or array is defined as a function of the preceding terms.
The term difference equation sometimes (and for the purposes of this article) refers to a specific type of recurrence relation. However, "difference equation" is frequently used to refer to any recurrence relation.
Examples
Logistic map
An example of a recurrence relation is the logistic map:
with a given constant r; given the initial term x0 each subsequent term is determined by this relation.
Some simply defined recurrence relations can have very complex (chaotic) behaviours, and they are a part of the field of mathematics known as nonlinear analysis.
Solving a recurrence relation means obtaining a closed-form solution: a non-recursive function of n.
Fibonacci numbers
The Fibonacci numbers are the archetype of a linear, homogeneous recurrence relation with constant coefficients (see below). They are defined using the linear recurrence relation
with seed values:
Explicitly, recurrence yields the equations:
etc.
We obtain the sequence of Fibonacci numbers, which begins:
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
It can be solved by methods described below yielding the closed-form expression, which involves powers of the two roots of the characteristic polynomial t2 = t + 1; the generating function of the sequence is the rational function
Binomial coefficients
A simple example of a multidimensional recurrence relation is given by the binomial coefficients  , which count the number of ways of selecting k out of a set of n elements.
They can be computed by the recurrence relation
, which count the number of ways of selecting k out of a set of n elements.
They can be computed by the recurrence relation
with the base cases 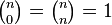 . Using this formula to compute the values of all binomial coefficients generates an infinite array called Pascal's triangle. The same values can also be computed directly by a different formula that is not a recurrence, but that requires multiplication and not just addition to compute:
. Using this formula to compute the values of all binomial coefficients generates an infinite array called Pascal's triangle. The same values can also be computed directly by a different formula that is not a recurrence, but that requires multiplication and not just addition to compute:
Structure
Linear homogeneous recurrence relations with constant coefficients
An order d linear homogeneous recurrence relation with constant coefficients is an equation of the form
where the d coefficients ci (for all i) are constants.
More precisely, this is an infinite list of simultaneous linear equations, one for each n>d−1. A sequence that satisfies a relation of this form is called a linear recurrence sequence or LRS. There are d degrees of freedom for LRS, i.e., the initial values 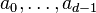 can be taken to be any values but then the linear recurrence determines the sequence uniquely.
can be taken to be any values but then the linear recurrence determines the sequence uniquely.
The same coefficients yield the characteristic polynomial (also "auxiliary polynomial")
whose d roots play a crucial role in finding and understanding the sequences satisfying the recurrence. If the roots r1, r2, ... are all distinct, then the solution to the recurrence takes the form
where the coefficients ki are determined in order to fit the initial conditions of the recurrence. When the same roots occur multiple times, the terms in this formula corresponding to the second and later occurrences of the same root are multiplied by increasing powers of n. For instance, if the characteristic polynomial can be factored as (x−r)3, with the same root r occurring three times, then the solution would take the form
As well as the Fibonacci numbers, other sequences generated by linear homogeneous recurrences include the Lucas numbers and Lucas sequences, the Jacobsthal numbers, the Pell numbers and more generally the solutions to Pell's equation.
Rational generating function
Theorem: Linear recursive sequences are precisely the sequences whose generating function is a rational function. The denominator is the polynomial obtained from the auxiliary polynomial by reversing the order of the coefficients, and the numerator is determined by the initial values of the sequence.[2]
The simplest cases are periodic sequences, 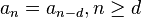 , which have sequence
, which have sequence 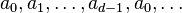 and generating function a sum of geometric series:
and generating function a sum of geometric series:
More generally, given the recurrence relation:
with generating function
the series is annihilated at ad and above by the polynomial:
That is, multiplying the generating function by the polynomial yields
as the coefficient on  , which vanishes (by the recurrence relation) for n ≥ d. Thus
, which vanishes (by the recurrence relation) for n ≥ d. Thus
so dividing yields
expressing the generating function as a rational function.
The denominator is 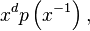 a transform of the auxiliary polynomial (equivalently, reversing the order of coefficients); one could also use any multiple of this, but this normalization is chosen both because of the simple relation to the auxiliary polynomial, and so that
a transform of the auxiliary polynomial (equivalently, reversing the order of coefficients); one could also use any multiple of this, but this normalization is chosen both because of the simple relation to the auxiliary polynomial, and so that 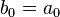 .
.
The generating function of the Catalan numbers is not a rational function, so the theorem tells us that the Catalan numbers do not satisfy a linear recurrence with constant coefficients.
Relationship to difference equations narrowly defined
Given an ordered sequence 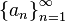 of real numbers: the first difference
of real numbers: the first difference 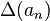 is defined as
is defined as
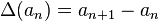 .
.
The second difference 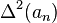 is defined as
is defined as
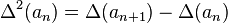 ,
,
which can be simplified to
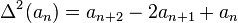 .
.
More generally: the kth difference of the sequence an is written as 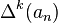 is defined recursively as
is defined recursively as
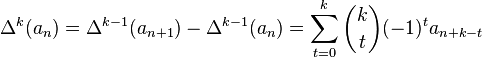 .
.
(The sequence and its differences are related by a binomial transform.) The more restrictive definition of difference equation is an equation composed of an and its kth differences. (A widely used broader definition treats "difference equation" as synonymous with "recurrence relation". See for example rational difference equation and matrix difference equation.)
Actually, it is easily seen that
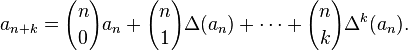 Thus, a difference equation can be defined as an equation that involves
an, an-1, an-2 etc. (or equivalenty
an, an+1, an+2 etc.)
Thus, a difference equation can be defined as an equation that involves
an, an-1, an-2 etc. (or equivalenty
an, an+1, an+2 etc.)
Since difference equations are a very common form of recurrence, some authors use the two terms interchangeably. For example, the difference equation
is equivalent to the recurrence relation
Thus one can solve many recurrence relations by rephrasing them as difference equations, and then solving the difference equation, analogously to how one solves ordinary differential equations. However, the Ackermann numbers are an example of a recurrence relation that do not map to a difference equation, much less points on the solution to a differential equation.
See time scale calculus for a unification of the theory of difference equations with that of differential equations.
Summation equations relate to difference equations as integral equations relate to differential equations.
From sequences to grids
Single-variable or one-dimensional recurrence relations are about sequences (i.e. functions defined on one-dimensional grids). Multi-variable or n-dimensional recurrence relations are about n-dimensional grids. Functions defined on n-grids can also be studied with partial difference equations.[3]
Solving
General methods
For order 1, the recurrence
has the solution an = rn with a0 = 1 and the most general solution is an = krn with a0 = k. The characteristic polynomial equated to zero (the characteristic equation) is simply t − r = 0.
Solutions to such recurrence relations of higher order are found by systematic means, often using the fact that an = rn is a solution for the recurrence exactly when t = r is a root of the characteristic polynomial. This can be approached directly or using generating functions (formal power series) or matrices.
Consider, for example, a recurrence relation of the form
When does it have a solution of the same general form as an = rn? Substituting this guess (ansatz) in the recurrence relation, we find that
must be true for all n > 1.
Dividing through by rn−2, we get that all these equations reduce to the same thing:
which is the characteristic equation of the recurrence relation. Solve for r to obtain the two roots λ1, λ2: these roots are known as the characteristic roots or eigenvalues of the characteristic equation. Different solutions are obtained depending on the nature of the roots: If these roots are distinct, we have the general solution
while if they are identical (when A2 + 4B = 0), we have
This is the most general solution; the two constants C and D can be chosen based on two given initial conditions a0 and a1 to produce a specific solution.
In the case of complex eigenvalues (which also gives rise to complex values for the solution parameters C and D), the use of complex numbers can be eliminated by rewriting the solution in trigonometric form. In this case we can write the eigenvalues as 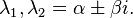 Then it can be shown that
Then it can be shown that
can be rewritten as[4]:576–585
where
Here E and F (or equivalently, G and δ) are real constants which depend on the initial conditions. Using
one may simplify the solution given above as
where a1 and a2 are the initial conditions and
In this way there is no need to solve for λ1 and λ2.
In all cases—real distinct eigenvalues, real duplicated eigenvalues, and complex conjugate eigenvalues—the equation is stable (that is, the variable a converges to a fixed value [specifically, zero]) if and only if both eigenvalues are smaller than one in absolute value. In this second-order case, this condition on the eigenvalues can be shown[5] to be equivalent to |A| < 1 − B < 2, which is equivalent to |B| < 1 and |A| < 1 − B.
The equation in the above example was homogeneous, in that there was no constant term. If one starts with the non-homogeneous recurrence
with constant term K, this can be converted into homogeneous form as follows: The steady state is found by setting bn = bn−1 = bn−2 = b* to obtain
Then the non-homogeneous recurrence can be rewritten in homogeneous form as
which can be solved as above.
The stability condition stated above in terms of eigenvalues for the second-order case remains valid for the general nth-order case: the equation is stable if and only if all eigenvalues of the characteristic equation are less than one in absolute value.
Solving via linear algebra
A linearly recursive sequence y of order n
is identical to
Expanded with n-1 identities of kind 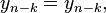 this n-th order equation is translated into a system of n first order linear equations,
this n-th order equation is translated into a system of n first order linear equations,
Observe that the vector 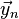 can be computed by n applications of the companion matrix, C, to the initial state vector,
can be computed by n applications of the companion matrix, C, to the initial state vector,  . Thereby, n-th entry of the sought sequence y, is the top component of
. Thereby, n-th entry of the sought sequence y, is the top component of ![\vec y_n, y_n = \vec y_n[n]](../I/m/d07999b88054bbc10eb979a8d58a88e2.png) .
.
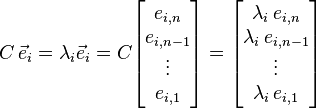
Eigendecomposition, 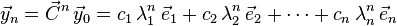 into eigenvalues,
into eigenvalues, 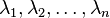 , and eigenvectors,
, and eigenvectors, 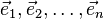 , is used to compute
, is used to compute 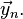 Thanks to the crucial fact that system C time-shifts every eigenvector, e, by simply scaling its components λ times,
Thanks to the crucial fact that system C time-shifts every eigenvector, e, by simply scaling its components λ times,
that is, time-shifted version of eigenvector,e, has components λ times larger, the eigenvector components are powers of λ, 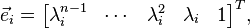 and, thus, recurrent linear homogeneous equation solution is a combination of exponential functions,
and, thus, recurrent linear homogeneous equation solution is a combination of exponential functions, 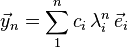 . The components
. The components 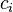 can be determined out of initial conditions:
can be determined out of initial conditions:
Solving for coefficients,
This also works with arbitrary boundary conditions 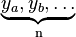 , not necessary the initial ones,
, not necessary the initial ones,
This description is really no different from general method above, however it is more succinct. It also works nicely for situations like
where there are several linked recurrences.[6]
Solving with z-transforms
Certain difference equations - in particular, linear constant coefficient difference equations - can be solved using z-transforms. The z-transforms are a class of integral transforms that lead to more convenient algebraic manipulations and more straightforward solutions. There are cases in which obtaining a direct solution would be all but impossible, yet solving the problem via a thoughtfully chosen integral transform is straightforward.
Theorem
Given a linear homogeneous recurrence relation with constant coefficients of order d, let p(t) be the characteristic polynomial (also "auxiliary polynomial")
such that each ci corresponds to each ci in the original recurrence relation (see the general form above). Suppose λ is a root of p(t) having multiplicity r. This is to say that (t−λ)r divides p(t). The following two properties hold:
- Each of the r sequences
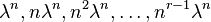 satisfies the recurrence relation.
satisfies the recurrence relation. - Any sequence satisfying the recurrence relation can be written uniquely as a linear combination of solutions constructed in part 1 as λ varies over all distinct roots of p(t).
As a result of this theorem a linear homogeneous recurrence relation with constant coefficients can be solved in the following manner:
- Find the characteristic polynomial p(t).
- Find the roots of p(t) counting multiplicity.
- Write an as a linear combination of all the roots (counting multiplicity as shown in the theorem above) with unknown coefficients bi.
- This is the general solution to the original recurrence relation. (q is the multiplicity of λ*)
- 4. Equate each
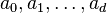 from part 3 (plugging in n = 0, ..., d into the general solution of the recurrence relation) with the known values
from part 3 (plugging in n = 0, ..., d into the general solution of the recurrence relation) with the known values 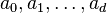 from the original recurrence relation. However, the values an from the original recurrence relation used do not usually have to be contiguous: excluding exceptional cases, just d of them are needed (i.e., for an original linear homogeneous recurrence relation of order 3 one could use the values a0, a1, a4). This process will produce a linear system of d equations with d unknowns. Solving these equations for the unknown coefficients
from the original recurrence relation. However, the values an from the original recurrence relation used do not usually have to be contiguous: excluding exceptional cases, just d of them are needed (i.e., for an original linear homogeneous recurrence relation of order 3 one could use the values a0, a1, a4). This process will produce a linear system of d equations with d unknowns. Solving these equations for the unknown coefficients 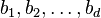 of the general solution and plugging these values back into the general solution will produce the particular solution to the original recurrence relation that fits the original recurrence relation's initial conditions (as well as all subsequent values
of the general solution and plugging these values back into the general solution will produce the particular solution to the original recurrence relation that fits the original recurrence relation's initial conditions (as well as all subsequent values 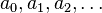 of the original recurrence relation).
of the original recurrence relation).
The method for solving linear differential equations is similar to the method above—the "intelligent guess" (ansatz) for linear differential equations with constant coefficients is eλx where λ is a complex number that is determined by substituting the guess into the differential equation.
This is not a coincidence. Considering the Taylor series of the solution to a linear differential equation:
it can be seen that the coefficients of the series are given by the nth derivative of f(x) evaluated at the point a. The differential equation provides a linear difference equation relating these coefficients.
This equivalence can be used to quickly solve for the recurrence relationship for the coefficients in the power series solution of a linear differential equation.
The rule of thumb (for equations in which the polynomial multiplying the first term is non-zero at zero) is that:
and more generally
Example: The recurrence relationship for the Taylor series coefficients of the equation:
is given by
or
This example shows how problems generally solved using the power series solution method taught in normal differential equation classes can be solved in a much easier way.
Example: The differential equation
has solution
The conversion of the differential equation to a difference equation of the Taylor coefficients is
It is easy to see that the nth derivative of eax evaluated at 0 is an
Solving non-homogeneous recurrence relations
If the recurrence is inhomogeneous, a particular solution can be found by the method of undetermined coefficients and the solution is the sum of the solution of the homogeneous and the particular solutions. Another method to solve an inhomogeneous recurrence is the method of symbolic differentiation. For example, consider the following recurrence:
This is an inhomogeneous recurrence. If we substitute n ↦ n+1, we obtain the recurrence
Subtracting the original recurrence from this equation yields
or equivalently
This is a homogeneous recurrence, which can be solved by the methods explained above. In general, if a linear recurrence has the form
where 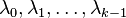 are constant coefficients and p(n) is the inhomogeneity, then if p(n) is a polynomial with degree r, then this inhomogeneous recurrence can be reduced to a homogeneous recurrence by applying the method of symbolic differencing r times.
are constant coefficients and p(n) is the inhomogeneity, then if p(n) is a polynomial with degree r, then this inhomogeneous recurrence can be reduced to a homogeneous recurrence by applying the method of symbolic differencing r times.
If
is the generating function of the inhomogeneity, the generating function
of the inhomogeneous recurrence
with constant coefficients ci is derived from
If P(x) is a rational generating function, A(x) is also one. The case discussed above, where pn = K is a constant, emerges as one example of this formula, with P(x) = K/(1−x). Another example, the recurrence 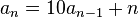 with linear inhomogeneity, arises in the definition of the schizophrenic numbers. The solution of homogeneous recurrences is incorporated as p = P = 0.
with linear inhomogeneity, arises in the definition of the schizophrenic numbers. The solution of homogeneous recurrences is incorporated as p = P = 0.
Solving first-order non-homogeneous recurrence relations with variable coefficients
Moreover, for the general first-order linear inhomogeneous recurrence relation with variable coefficients:
there is also a nice method to solve it:[7]
Let
Then
General linear homogeneous recurrence relations
Many linear homogeneous recurrence relations may be solved by means of the generalized hypergeometric series. Special cases of these lead to recurrence relations for the orthogonal polynomials, and many special functions. For example, the solution to
is given by
the Bessel function, while
is solved by
the confluent hypergeometric series.
Solving a first order rational difference equation
A first order rational difference equation has the form 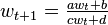 . Such an equation can be solved by writing
. Such an equation can be solved by writing 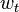 as a nonlinear transformation of another variable
as a nonlinear transformation of another variable  which itself evolves linearly. Then standard methods can be used to solve the linear difference equation in
which itself evolves linearly. Then standard methods can be used to solve the linear difference equation in  .
.
Stability
Stability of linear higher-order recurrences
The linear recurrence of order d,
has the characteristic equation
The recurrence is stable, meaning that the iterates converge asymptotically to a fixed value, if and only if the eigenvalues (i.e., the roots of the characteristic equation), whether real or complex, are all less than unity in absolute value.
Stability of linear first-order matrix recurrences
In the first-order matrix difference equation
with state vector x and transition matrix A, x converges asymptotically to the steady state vector x* if and only if all eigenvalues of the transition matrix A (whether real or complex) have an absolute value which is less than 1.
Stability of nonlinear first-order recurrences
Consider the nonlinear first-order recurrence
This recurrence is locally stable, meaning that it converges to a fixed point x* from points sufficiently close to x*, if the slope of f in the neighborhood of x* is smaller than unity in absolute value: that is,
A nonlinear recurrence could have multiple fixed points, in which case some fixed points may be locally stable and others locally unstable; for continuous f two adjacent fixed points cannot both be locally stable.
A nonlinear recurrence relation could also have a cycle of period k for k > 1. Such a cycle is stable, meaning that it attracts a set of initial conditions of positive measure, if the composite function
with f appearing k times is locally stable according to the same criterion:
where x* is any point on the cycle.
In a chaotic recurrence relation, the variable x stays in a bounded region but never converges to a fixed point or an attracting cycle; any fixed points or cycles of the equation are unstable. See also logistic map, dyadic transformation, and tent map.
Relationship to differential equations
When solving an ordinary differential equation numerically, one typically encounters a recurrence relation. For example, when solving the initial value problem
with Euler's method and a step size h, one calculates the values
by the recurrence
Systems of linear first order differential equations can be discretized exactly analytically using the methods shown in the discretization article.
Applications
Biology
Some of the best-known difference equations have their origins in the attempt to model population dynamics. For example, the Fibonacci numbers were once used as a model for the growth of a rabbit population.
The logistic map is used either directly to model population growth, or as a starting point for more detailed models. In this context, coupled difference equations are often used to model the interaction of two or more populations. For example, the Nicholson-Bailey model for a host-parasite interaction is given by
with Nt representing the hosts, and Pt the parasites, at time t.
Integrodifference equations are a form of recurrence relation important to spatial ecology. These and other difference equations are particularly suited to modeling univoltine populations.
Computer science
Recurrence relations are also of fundamental importance in analysis of algorithms.[8][9] If an algorithm is designed so that it will break a problem into smaller subproblems (divide and conquer), its running time is described by a recurrence relation.
A simple example is the time an algorithm takes to find an element in an ordered vector with  elements, in the worst case.
elements, in the worst case.
A naive algorithm will search from left to right, one element at a time. The worst possible scenario is when the required element is the last, so the number of comparisons is  .
.
A better algorithm is called binary search. However, it requires a sorted vector. It will first check if the element is at the middle of the vector. If not, then it will check if the middle element is greater or lesser than the sought element. At this point, half of the vector can be discarded, and the algorithm can be run again on the other half. The number of comparisons will be given by
which will be close to 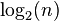 .
.
Digital signal processing
In digital signal processing, recurrence relations can model feedback in a system, where outputs at one time become inputs for future time. They thus arise in infinite impulse response (IIR) digital filters.
For example, the equation for a "feedforward" IIR comb filter of delay T is:
Where  is the input at time t,
is the input at time t,  is the output at time t, and α controls how much of the delayed signal is fed back into the output. From this we can see that
is the output at time t, and α controls how much of the delayed signal is fed back into the output. From this we can see that
etc.
Economics
Recurrence relations, especially linear recurrence relations, are used extensively in both theoretical and empirical economics.[10] In particular, in macroeconomics one might develop a model of various broad sectors of the economy (the financial sector, the goods sector, the labor market, etc.) in which some agents' actions depend on lagged variables. The model would then be solved for current values of key variables (interest rate, real GDP, etc.) in terms of exogenous variables and lagged endogenous variables. See also time series analysis.
See also
- Holonomic sequences
- Iterated function
- Matrix difference equation
- Orthogonal polynomials
- Recursion
- Recursion (computer science)
- Lagged Fibonacci generator
- Master theorem
- Circle points segments proof
- Continued fraction
- Time scale calculus
- Integrodifference equation
- Combinatorial principles
- Infinite impulse response
Notes
- ↑ Greene, Daniel H.; Knuth, Donald E. (1982), "2.1.1 Constant coefficients – A) Homogeneous equations", Mathematics for the Analysis of Algorithms (2nd ed.), Birkhäuser, p. 17.
- ↑ Martino, Ivan; Martino, Luca (2013-11-14). "On the variety of linear recurrences and numerical semigroups". Semigroup Forum 88 (3): 569–574. doi:10.1007/s00233-013-9551-2. ISSN 0037-1912.
- ↑ Partial difference equations, Sui Sun Cheng, CRC Press, 2003, ISBN 978-0-415-29884-1
- ↑ Chiang, Alpha C., Fundamental Methods of Mathematical Economics, third edition, McGraw-Hill, 1984.
- ↑ Papanicolaou, Vassilis, "On the asymptotic stability of a class of linear difference equations," Mathematics Magazine 69(1), February 1996, 34–43.
- ↑ Maurer, Stephen B.; Ralston, Anthony (1998), Discrete Algorithmic Mathematics (2nd ed.), A K Peters, p. 609, ISBN 9781568810911.
- ↑ http://faculty.pccu.edu.tw/%7Emeng/Math15.pdf
- ↑ Cormen, T. et al, Introduction to Algorithms, MIT Press, 2009
- ↑ R. Sedgewick, F. Flajolet, An Introduction to the Analysis of Algorithms, Addison-Wesley, 2013
- ↑ Sargent, Thomas J., Dynamic Macroeconomic Theory, Harvard University Press, 1987.
References
- Batchelder, Paul M. (1967). An introduction to linear difference equations. Dover Publications.
- Miller, Kenneth S. (1968). Linear difference equations. W. A. Benjamin.
- Fillmore, Jay P.; Marx, Morris L. (1968). "Linear recursive sequences". SIAM Rev. 10 (3). pp. 324–353. JSTOR 2027658.
- Brousseau, Alfred (1971). Linear Recursion and Fibonacci Sequences. Fibonacci Association.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 1990. ISBN 0-262-03293-7. Chapter 4: Recurrences, pp. 62–90.
- Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994). Concrete Mathematics: A Foundation for Computer Science (2 ed.). Addison-Welsey. ISBN 0-201-55802-5.
- Enders, Walter (2010). Applied Econometric Times Series (3 ed.).
- Cull, Paul; Flahive, Mary; Robson, Robbie (2005). Difference Equations: From Rabbits to Chaos. Springer. ISBN 0-387-23234-6. chapter 7.
- Jacques, Ian (2006). Mathematics for Economics and Business (Fifth ed.). Prentice Hall. pp. 551–568. ISBN 0-273-70195-9. Chapter 9.1: Difference Equations.
- Minh, Tang; Van To, Tan (2006). "Using generating functions to solve linear inhomogeneous recurrence equations" (PDF). Proc. Int. Conf. Simulation, Modelling and Optimization, SMO'06. pp. 399–404.
- Polyanin, Andrei D. "Difference and Functional Equations: Exact Solutions". at EqWorld - The World of Mathematical Equations.
- Polyanin, Andrei D. "Difference and Functional Equations: Methods". at EqWorld - The World of Mathematical Equations.
- Wang, Xiang-Sheng; Wong, Roderick (2012). "Asymptotics of orthogonal polynomials via recurrence relations". Anal. Appl. 10 (2): 215–235. doi:10.1142/S0219530512500108.
External links
- Hazewinkel, Michiel, ed. (2001), "Recurrence relation", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W., "Recurrence Equation", MathWorld.
- Mathews, John H. "Homogeneous Difference Equations".
- "OEIS Index Rec". OEIS index to a few thousand examples of linear recurrences, sorted by order (number of terms) and signature (vector of values of the constant coefficients)
|
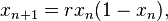
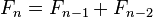
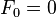

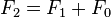
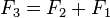
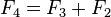
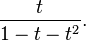
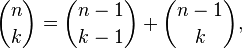
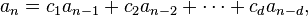

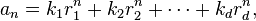
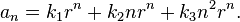
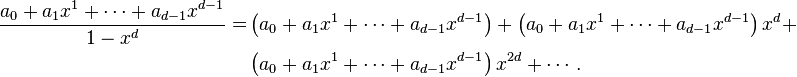
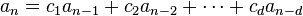
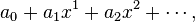
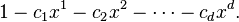
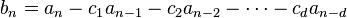
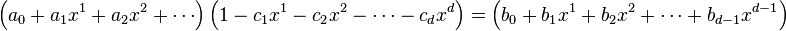
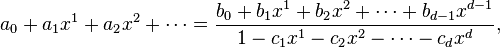
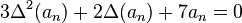
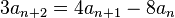
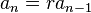
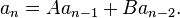
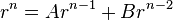
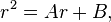
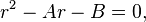
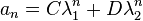
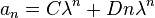
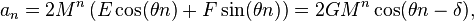
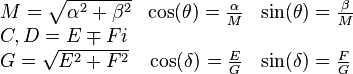
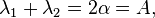
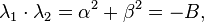
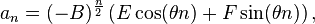
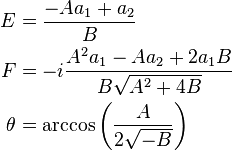

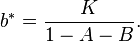
![[b_n - b^*]=A[b_{n-1}-b^*]+B[b_{n-2}-b^*],](../I/m/094ba9f73ab0ff2f69e0af404c29b7b6.png)
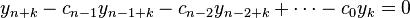
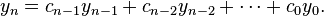
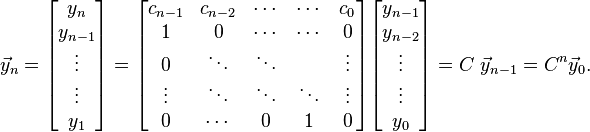
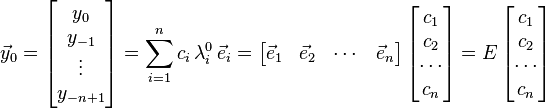
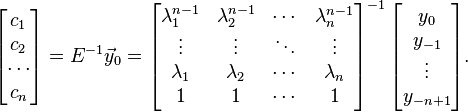
![\begin{bmatrix}y_a \\ y_b \\ \vdots\end{bmatrix} = \begin{bmatrix}\vec y_a[n] \\ \vec y_b[n] \\ \vdots\end{bmatrix} = \begin{bmatrix}\sum_{i=1}^n {c_i\,\lambda_i^a\,\vec e_i[n]} \\ \sum_{i=1}^n {c_i\,\lambda_i^b\,\vec e_i[n]} \\ \vdots\end{bmatrix} =\begin{bmatrix}\sum_{i=1}^n {c_i\,\lambda_i^a\,\lambda_i^{n-1}} \\ \sum_{i=1}^n {c_i\,\lambda_i^b\,\lambda_i^{n-1}} \\ \vdots\end{bmatrix} =](../I/m/cf8e9634cce1bd2996936fcb09097a0d.png)
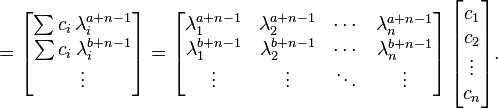
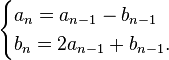
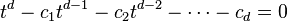
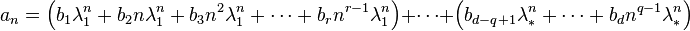
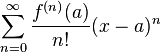
![y^{[k]} \to f[n+k]](../I/m/19d7803b0166b65a77fe2970279cc30e.png)
![x^m*y^{[k]} \to n(n-1)(n-m+1)f[n+k-m]](../I/m/0acc80c8056f394455dfa25158339a69.png)
![(x^2 + 3x -4)y^{[3]} -(3x+1)y^{[2]} + 2y = 0](../I/m/3dfa6e42793e87136f96d2ad6f1e2f18.png)
![n(n-1)f[n+1] + 3nf[n+2] -4f[n+3] -3nf[n+1] -f[n+2]+ 2f[n] = 0](../I/m/3ad6ac7bcc0519a444a68dba649b8c3a.png)
![-4f[n+3] +2nf[n+2] + n(n-4)f[n+1] +2f[n] = 0.](../I/m/e66c8fa45175142a88f80f64183f8eac.png)
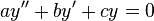
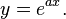
![af[n + 2] + bf[n + 1] + cf[n] = 0.](../I/m/a3286dd08292be8e91efeedcc3fdb392.png)
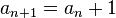
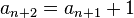
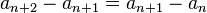
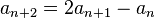
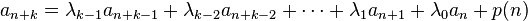
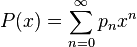
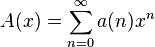
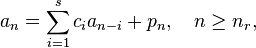
![\left (1-\sum_{i=1}^sc_ix^i \right )A(x)=P(x)+\sum_{n=0}^{n_r-1}[a_n-p_n]x^n-\sum_{i=1}^s c_ix^i\sum_{n=0}^{n_r-i-1}a_nx^n.](../I/m/6a58cc872bda2ce8810c36241838ceeb.png)
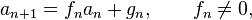
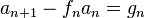
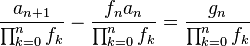
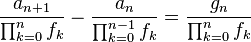
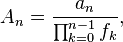
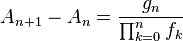
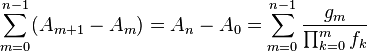
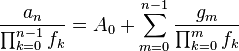
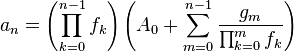
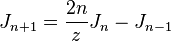
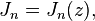
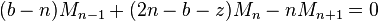
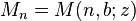
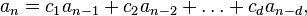
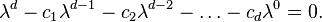
![[x_t - x^*] = A[x_{t-1}-x^*]\,](../I/m/00f95c038edd8d116d962d507f79c874.png)