Recoil temperature

In laser cooling, the Boltzmann constant times the recoil temperature is equal to the recoil energy deposited in a single atom initially at rest by the spontaneous emission of a single photon.^[1] The recoil temperature is

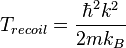$T_{recoil}=\frac{\hbar^2k^2}{2mk_B}$ ,

since the photon's momentum is 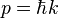$p = \hbar k$ (here $k$ is the wavevector of the light, $m$ is the mass of an atom, 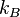$k_B$ is Boltzmann's constant and 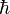$\hbar$ is Planck's constant). The recoil temperature for the D2 lines of alkali atoms is typically on the order of 1 μK, and thus lower than the Doppler temperature.^[2] An example of a process where the recoil temperature can be reached is Sisyphus cooling.^[3]

See also: Doppler cooling and Mössbauer effect

References

↑ Metcalf and van der Straten (1999). Laser Cooling and Trapping. New York: Springer-Verlag. ISBN 0-387-98728-2.
↑ Cohen-Tannoudji, Claude N. (1 July 1998). "Nobel Lecture: Manipulating atoms with photons". Reviews of Modern Physics 70 (3): 707–719. doi:10.1103/RevModPhys.70.707.
↑ Cohen-Tannoudji, C. (2004). Atoms in electromagnetic fields (2nd ed.). Singapore: World Scientific. ISBN 978-9812560193.

This article is issued from Wikipedia - version of the Wednesday, September 23, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.