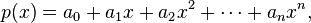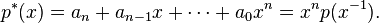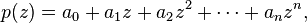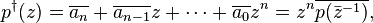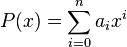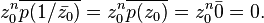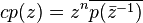Reciprocal polynomial

In algebra, the reciprocal polynomial $p *$ of a polynomial $p$ of degree $n$ with coefficients from an arbitrary field, such as

p(x) = a_0 + a_1x + a_2x^2 + \cdots + a_nx^n, \,\!

is the polynomial^[1]

p^*(x) = a_n + a_{n-1}x + \cdots + a_0x^n = x^n p(x^{-1}).

Essentially, the coefficients are written in reverse order. They arise naturally in linear algebra as the characteristic polynomial of the inverse of a matrix.

In the special case that the polynomial $p$ has complex coefficients, that is,

p(z) = a_0 + a_1z + a_2z^2 + \cdots + a_nz^n, \,\!

the conjugate reciprocal polynomial, $p †$ given by,

p^{\dagger}(z) = \overline{a_n} + \overline{a_{n-1}}z + \cdots + \overline{a_0}z^n = z^n\overline{p(\bar{z}^{-1})},

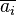where $\overline{a_i}$ denotes the complex conjugate of 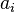$a_i \,\!$ , is also called the reciprocal polynomial when no confusion can arise.

A polynomial $p$ is called self-reciprocal if $p (x) = p * (x)$ .

The coefficients of a self-reciprocal polynomial satisfy $a i = a n - i$ , and in this case $p$ is also called a palindromic polynomial. In the conjugate reciprocal case, the coefficients must be real to satisfy the condition.

Properties

Reciprocal polynomials have several connections with their original polynomials, including:

$α$ is a root of polynomial $p$ if and only if $α -1$ is a root of $p *$ .^[2]
If $p (x) \neq x$ then $p$ is irreducible if and only if $p *$ is irreducible.^[3]
$p$ is primitive if and only if $p *$ is primitive.^[2]

Other properties of reciprocal polynomials may be obtained, for instance:

If a polynomial is self-reciprocal and irreducible then it must have even degree.^[3]

Palindromic and antipalindromic polynomials

A self-reciprocal polynomial is called palindromic because its coefficients, when the polynomial is written in ascending or descending order, form a palindrome. That is, if

P(x) = \sum_{i=0}^n a_ix^i

is a polynomial of degree $n$ , then $P$ is palindromic if $a i = a n - i$ for $i = 0, 1, ..., n$ . Some authors use the terms "palindromic" and "reciprocal" interchangeably.

Similarly, $P$ , a polynomial of degree $n$ , is called antipalindromic if $a i = - a n - i$ for $i = 0, 1, ... n$ . That is, a polynomial $P$ is antipalindromic if $P (x) = - P * (x)$ .

Due to the properties of the binomial coefficients the polynomials $P (x) = (x + 1 ) n$ are palindromic for all positive integers $n$ , while the polynomials $Q (x) = (x - 1 ) n$ are palindromic when $n$ is even and antipalindromic when $n$ is odd. Also, cyclotomic polynomials are palindromic.

General properties

If $a$ is a root of a polynomial that is either palindromic or antipalindromic, then 1/ $a$ is also a root and has the same multiplicity.^[4]
The converse is true: If a polynomial is such that if $a$ is a root then 1/ $a$ is also a root of the same multiplicity, then the polynomial is either palindromic or antipalindromic.
For any polynomial $q$ , the polynomial $q + q *$ is palindromic and the polynomial $q - q *$ is antipalindromic.
Any polynomial $q$ can be written as the sum of a palindromic and an antipalindromic polynomial.^[5]
The product of two palindromic or antipalindromic polynomials is palindromic.
The product of a palindromic polynomial and an antipalindromic polynomial is antipalindromic.
A palindromic polynomial of odd degree is a multiple of $x + 1$ (it has -1 as a root) and its quotient by $x + 1$ is also palindromic.
An antipalindromic polynomial is a multiple of $x - 1$ (it has 1 as a root) and its quotient by $x - 1$ is palindromic.
An antipalindromic polynomial of even degree is a multiple of $x 2 - 1$ (it has -1 and 1 as a roots) and its quotient by $x 2 - 1$ is palindromic.
If $p (x)$ is a palindromic polynomial of even degree $2d$ , then there is a polynomial $q$ of degree $d$ such that $p (x) = x d q (x + 1 / x)$ .
If $p (x)$ is a monic antipalindromic polynomial of even degree $2d$ over a field $k$ with odd characteristic, then it can be written uniquely as $p (x) = x d (Q (x) - Q (1 / x))$ , where $Q$ is a monic polynomial of degree $d$ with no constant term.^[6]

It follows from the definition that if $P$ is of even degree $n$ (so it has an odd number of terms), then it can only be antipalindromic when the "middle" term is 0, i.e., $a m = - a n - m$ , where $n = 2 m$ .

Real coefficients

A polynomial with real coefficients all of whose complex roots lie on the unit circle in the complex plane (all the roots are unimodular) is either palindromic or antipalindromic.^[7]

Conjugate reciprocal polynomials

A polynomial is conjugate reciprocal if 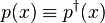$p(x) \equiv p^{\dagger}(x)$ and self-inversive if 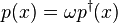$p(x) = \omega p^{\dagger}(x)$ for a scale factor $ω$ on the unit circle.^[8]

If $p (z)$ is the minimal polynomial of $z 0$ with $| z 0 | = 1, z 0 \neq 1$ , and $p (z)$ has real coefficients, then $p (z)$ is self-reciprocal. This follows because

z_0^n\overline{p(1/\bar{z_0})} = z_0^n\overline{p(z_0)} = z_0^n\bar{0} = 0.

So $z 0$ is a root of the polynomial 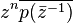$z^n\overline{p(\bar{z}^{-1})}$ which has degree $n$ . But, the minimal polynomial is unique, hence

cp(z) = z^n\overline{p(\bar{z}^{-1})}

for some constant $c$ , i.e. 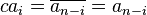$ca_i=\overline{a_{n-i}}=a_{n-i}$ . Sum from $i = 0$ to $n$ and note that 1 is not a root of $p$ . We conclude that $c = 1$ .

A consequence is that the cyclotomic polynomials $Φ n$ are self-reciprocal for $n > 1$ . This is used in the special number field sieve to allow numbers of the form $x 11 \pm 1, x 13 \pm 1, x 15 \pm 1$ and $x 21 \pm 1$ to be factored taking advantage of the algebraic factors by using polynomials of degree 5, 6, 4 and 6 respectively – note that $φ$ (Euler's totient function) of the exponents are 10, 12, 8 and 12.

Application in coding theory

The reciprocal polynomial finds a use in the theory of cyclic error correcting codes. Suppose $x n - 1$ can be factored into the product of two polynomials, say $x n - 1 = g (x) p (x)$ . When $g (x)$ generates a cyclic code $C$ , then the reciprocal polynomial $p *$ generates $C ⊥$ , the orthogonal complement of $C$ .^[9] Also, $C$ is self-orthogonal (that is, $C \subseteq C ⊥)$ , if and only if $p *$ divides $g (x)$ .^[10]

Notes

↑ Roman 1995, pg.37
1 2 Pless 1990, pg. 57
1 2 Roman 1995, pg. 37
↑ Pless 1990, pg. 57 for the palindromic case only
↑ Stein, Jonathan Y. (2000), Digital Signal Processing: A Computer Science Perspective, Wiley Interscience, p. 384, ISBN 9780471295464
↑ Katz, Nicholas M. (2012), Convolution and Equidistribution : Sato-Tate Theorems for Finite Field Mellin Transformations, Princeton University Press, p. 146, ISBN 9780691153315
↑ Markovsky, Ivan; Rao, Shodhan (2008), "Palindromic polynomials, time-reversible systems and conserved quantities", Control and Automation, doi:10.1109/MED.2008.4602018
↑ Sinclair, Christopher D.; Vaaler, Jeffrey D. (2008). "Self-inversive polynomials with all zeros on the unit circle". In McKee, James; Smyth, C. J. Number theory and polynomials. Proceedings of the workshop, Bristol, UK, April 3–7, 2006. London Mathematical Society Lecture Note Series 352. Cambridge: Cambridge University Press. pp. 312–321. ISBN 978-0-521-71467-9. Zbl 06093092.
↑ Pless 1990, pg. 75, Theorem 48
↑ Pless 1990, pg. 77, Theorem 51

References

Pless, Vera (1990), Introduction to the Theory of Error Correcting Codes (2nd ed.), New York: Wiley-Interscience, ISBN 0-471-61884-5

Roman, Steven (1995), Field Theory, New York: Springer-Verlag, ISBN 0-387-94408-7

External links

"The Fundamental Theorem for Palindromic Polynomials" at MathPages.com.
Reciprocal Polynomial (on MathWorld)

This article is issued from Wikipedia - version of the Wednesday, September 30, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.