Real closed ring

In mathematics, a real closed ring is a commutative ring A that is a subring of a product of real closed fields, which is closed under continuous semi-algebraic functions defined over the integers.

Examples of real closed rings

Since the rigorous definition of a real closed ring is of technical nature it is convenient to see a list of prominent examples first. The following rings are all real closed rings:

real closed fields. These are exactly the real closed rings that are fields.
the ring of all real valued continuous functions on a completely regular space X. Also, the ring of all bounded real valued continuous functions on X is real closed.
convex subrings of real closed fields. These are precisely those real closed rings which are also valuation rings and were initially studied by Cherlin and Dickmann (they used the term 'real closed ring' for what is now called 'real closed valuation ring').
the ring A of all continuous semi-algebraic functions on a semi-algebraic set of a real closed field (with values in that field). Also, the subring of all bounded (in any sense) functions in A is real closed.
(generalizing the previous example) the ring of all (bounded) continuous definable functions on a definable set S of an arbitrary first-order expansion M of a real closed field (with values in M). Also, the ring of all (bounded) definable functions 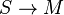$S\to M$ is real closed.
Real closed rings are precisely the rings of global sections of affine real closed spaces (a generalization of semialgebraic spaces) and in this context they were invented by Niels Schwartz in the early 1980s.

Definition

A real closed ring is a reduced, commutative unital ring A which has the following properties:

The set of squares of A is the set of nonnegative elements of a partial order ≤ on A and (A,≤) is an f-ring.
Convexity condition: For all a,b from A, if 0≤a≤b then b|a².
For every prime ideal p of A, the residue class ring A/p is integrally closed and its field of fractions is a real closed field.

The link to the definition at the beginning of this article is given in the section on algebraic properties below.

The real closure of a commutative ring

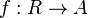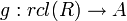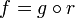Every commutative unital ring R has a so-called real closure rcl(R) and this is unique up to a unique ring homomorphism over R. This means that rcl(R) is a real closed ring and there is a (not necessarily injective) ring homomorphism $r:R\to rcl(R)$ such that for every ring homomorphism $f:R\to A$ to some other real closed ring A, there is a unique ring homomorphism $g:rcl(R)\to A$ with $f=g\circ r$ .

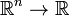For example the real closure of the polynomial ring $\mathbb{R}[T_1,...,T_n]$ is the ring of continuous semi-algebraic functions $\mathbb{R}^n\to \mathbb{R}$ .

Note that an arbitrary ring R is semi-real (i.e. -1 is not a sum of squares in R) if and only if the real closure of R is not the null ring.

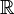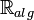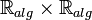Note also that the real closure of an ordered field is in general not the real closure of the underlying field. For example, the real closure of the ordered subfield $\mathbb{Q}(\sqrt 2)$ of $\mathbb{R}$ is the field $\mathbb{R}_{alg}$ of real algebraic numbers, whereas the real closure of the field $\mathbb{Q}(\sqrt 2)$ is the ring $\mathbb{R}_{alg}\times \mathbb{R}_{alg}$ (corresponding to the two orders of $\mathbb{Q}(\sqrt 2)$ ). More generally the real closure of a field F is a certain subdirect product of the real closures of the ordered fields (F,P), where P runs through the orderings of F.

Algebraic properties

The category RCR of real closed rings which has real closed rings as objects and ring homomorphisms as maps has the following properties:

Arbitrary products, direct limits and inverse limits (in the category of commutative unital rings) of real closed rings are again real closed. The fibre sum of two real closed rings B,C over some real closed ring A exists in RCR and is the real closure of the tensor product of B and C over A.
RCR has arbitrary limits and co-limits.
RCR is a variety in the sense of universal algebra (but not a subvariety of commutative rings).

For a real closed ring A, the natural homomorphism of A to the product of all its residue fields is an isomorphism onto a subring of this product that is closed under continuous semi-algebraic functions defined over the integers. Conversely, every subring of a product of real closed fields with this property is real closed.
If I is a radical ideal of a real closed ring A, then also the residue class ring A/I is real closed. If I and J are radical ideals of a real closed ring then the sum I + J is again a radical ideal.
All classical localizations S⁻¹A of a real closed ring A are real closed. The epimorphic hull and the complete ring of quotients of a real closed ring are again real closed.
The (real) holomorphy ring H(A) of a real closed ring A is again real closed. By definition, H(A) consists of all elements f in A with the property −N ≤ f ≤ N for some natural number N. Applied to the examples above, this means that the rings of bounded (semi-algebraic/definable) continuous functions are all real closed.
The support map from the real spectrum of a real closed ring to its Zariski spectrum, which sends an ordering P to its support 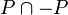$P\cap -P$ is a homeomorphism. In particular, the Zariski spectrum of every real closed ring A is a root system (in the sense of graph theory) and therefore A is also a Gel'fand ring (i.e. every prime ideal of A is contained in a unique maximal ideal of A). The comparison of the Zariski spectrum of A with the Zariski spectrum of H(A) leads to a homeomorphism between the maximal spectra of these rings, generalizing the Gel'fand-Kolmogorov theorem for rings of real valued continuous functions.
The natural map r from an arbitrary ring R to its real closure rcl(R) as explained above, induces a homeomorphism from the real spectrum of rcl(R) to the real spectrum of R.
Summarising and significantly strengthening the previous two properties, the following is true: The natural map r from an arbitrary ring R to its real closure rcl(R) induces an identification of the affine scheme of rcl(R) with the affine real closed space of R.
Every local real closed ring is a Henselian ring (but in general local real closed domains are not valuation rings).

Model theoretic properties

The class of real closed rings is first-order axiomatizable and undecidable. The class of all real closed valuation rings is decidable (by Cherlin-Dickmann) and the class of all real closed fields is decidable (by Tarski). After naming a definable radical relation, real closed rings have a model companion, namely von Neumann regular real closed rings.

Comparison with characterizations of real closed fields

There are many different characterizations of real closed fields. For example in terms of maximality (with respect to algebraic extensions): a real closed field is a maximally orderable field; or, a real closed field (together with its unique ordering) is a maximally ordered field. Another characterization says that the intermediate value theorem holds for all polynomials in one variable over the (ordered) field. In the case of commutative rings, all these properties can be (and are) analyzed in the literature. They all lead to different classes of rings which are unfortunately also called 'real closed' (because a certain characterization of real closed fields has been extended to rings). None of them lead to the class of real closed rings and none of them allow a satisfactory notion of a closure operation. A central point in the definition of real closed rings is the globalisation of the notion of a real closed field to rings when these rings are represented as rings of functions on some space (typically, the real spectrum of the ring).

References

Cherlin, Gregory. Rings of continuous functions: decision problems Model theory of algebra and arithmetic (Proc. Conf., Karpacz, 1979), pp. 44–91, Lecture Notes in Math., 834, Springer, Berlin, 1980.
Cherlin, Gregory(1-RTG2); Dickmann, Max A. Real closed rings. II. Model theory. Ann. Pure Appl. Logic 25 (1983), no. 3, 213–231.
A. Prestel, N. Schwartz. Model theory of real closed rings. Valuation theory and its applications, Vol. I (Saskatoon, SK, 1999), 261–290, Fields Inst. Commun., 32, Amer. Math. Soc., Providence, RI, 2002.
Schwartz, Niels. The basic theory of real closed spaces. Memoirs of the American Mathematical Society 1989 (ISBN 0821824600 )
Schwartz, Niels; Madden, James J. Semi-algebraic function rings and reflectors of partially ordered rings. Lecture Notes in Mathematics, 1712. Springer-Verlag, Berlin, 1999
Schwartz, Niels. Real closed rings. Algebra and order (Luminy-Marseille, 1984), 175–194, Res. Exp. Math., 14, Heldermann, Berlin, 1986
Schwartz, Niels. Rings of continuous functions as real closed rings. Ordered algebraic structures (Curaçao, 1995), 277–313, Kluwer Acad. Publ., Dordrecht, 1997.
Tressl, Marcus. Super real closed rings. Fundamenta Mathematicae 194 (2007), no. 2, 121–177.

This article is issued from Wikipedia - version of the Sunday, January 24, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.