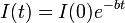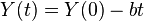Reactive inhibition
Reactive inhibition is a phrase coined by Clark L. Hull (1951) in his postulate X.A.:
Whenever a reaction R is evoked from an organism there is left an increment of primary negative drive IR which inhibits to a degree according to its magnitude the reaction potential SER to that response (Hull, 1951, p. 74).
According to Hull's postulate X.B. inhibition I dissipates exponentially with time t:.:
With the passage of time since its formation IR spontaneously dissipates approximately as a simple decay function of the time t elapsed, i.e.,
(Hull, 1951, p. 74).
Hull's decay formula is somewhat awkward and might give rise to confusion. For example, I'R does not refer to the derivative of IR. A more convenient way of writing the formula would be as follows:
with 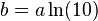 .
. 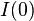 is the inhibition at the beginning the time interval [0,t]. Note, that if one takes the natural logarithm of both sides one obtains:
is the inhibition at the beginning the time interval [0,t]. Note, that if one takes the natural logarithm of both sides one obtains:
where 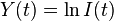 and
and 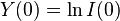 . The last formula is used in Inhibition Theory.
. The last formula is used in Inhibition Theory.
References
Hull, C.L.: Essentials of behavior. Westport (Connecticut): Greenwood Press, 1951.
This article is issued from Wikipedia - version of the Saturday, July 21, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.