Reactive programming
In computing, reactive programming is a programming paradigm oriented around data flows and the propagation of change. This means that it should be possible to express static or dynamic data flows with ease in the programming languages used, and that the underlying execution model will automatically propagate changes through the data flow.
For example, in an imperative programming setting, 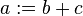 would mean that
would mean that  is being assigned the result of
is being assigned the result of 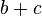 in the instant the expression is evaluated, and later, the values of
in the instant the expression is evaluated, and later, the values of  and
and  can be changed with no effect on the value of
can be changed with no effect on the value of  .
.
However, in reactive programming, the value of  would be automatically updated based on the new values, the opposite of functional programming.
would be automatically updated based on the new values, the opposite of functional programming.
A modern spreadsheet program is an example of reactive programming. Spreadsheet cells can contain literal values, or formulas such as "=B1+C1" that are evaluated based on other cells. Whenever the value of the other cells change, the value of the formula is automatically updated.
Another example is a hardware description language such as Verilog. In this case, reactive programming allows changes to be modeled as they propagate through a circuit.
Reactive programming has foremost been proposed as a way to simplify the creation of interactive user interfaces, animations in real time systems, but is essentially a general programming paradigm.
For example, in a Model-view-controller architecture, reactive programming can allow changes in the underlying model to automatically be reflected in the view, and vice versa.[1]
Concepts
Degrees of explicitness
Reactive programming languages can range from very explicit ones where data flows are set up by using arrows, to implicit where the data flows are derived from language constructs that look similar to those of imperative or functional programming. For example, in implicitly lifted functional reactive programming (FRP) a function call might implicitly cause a node in a data flow graph to be constructed. Reactive programming libraries for dynamic languages (such as the Lisp "Cells" and Python "Trellis" libraries) can construct a dependency graph from runtime analysis of the values read during a function's execution, allowing data flow specifications to be both implicit and dynamic.
Sometimes the term reactive programming refers to the architectural level of software engineering, where individual nodes in the data flow graph are ordinary programs that communicate with each other.
Static or Dynamic
Reactive programming can be purely static where the data flows are set up statically, or be dynamic where the data flows can change during the execution of a program.
The use of data switches in the data flow graph could to some extent make a static data flow graph appear as dynamic, and blur the distinction slightly. True dynamic reactive programming however could use imperative programming to reconstruct the data flow graph.
Higher-order reactive programming
Reactive programming could be said to be of higher order if it supports the idea that data flows could be used to construct other data flows. That is, the resulting value out of a data flow is another data flow graph that is executed using the same evaluation model as the first.
Data flow differentiation
Ideally all data changes are propagated instantly, but this cannot be assured in practice. Instead it might be necessary to give different parts of the data flow graph different evaluation priorities. This can be called differentiated reactive programming.
For example, in a word processor the marking of spelling errors need not be totally in sync with the inserting of characters. Here differentiated reactive programming could potentially be used to give the spell checker lower priority, allowing it to be delayed while keeping other data-flows instantaneous.
However, such differentiation introduces additional design complexity. For example, deciding how to define the different data flow areas, and how to handle event passing between different data flow areas.
Evaluation models of reactive programming
Evaluation of reactive programs is not necessarily based on how stack based programming languages are evaluated. Instead, when some data is changed, the change is propagated to all data that is derived partially or completely from the data that was changed. This change propagation could be achieved in a number of ways, where perhaps the most natural way is an invalidate/lazy-revalidate scheme.
It could be problematic to just naively propagate a change using a stack, because of potential exponential update complexity if the data structure has a certain shape. One such shape can be described as "repeated diamonds shape", and has the following structure: An→Bn→An+1, An→Cn→An+1, where n=1,2... This problem could be overcome by propagating invalidation only when some data is not already invalidated, and later re-validate the data when needed using lazy evaluation.
One inherent problem for reactive programming is that most computations that would be evaluated and forgotten in a normal programming language, needs to be represented in the memory as data-structures. This could potentially make RP highly memory consuming. However, research on what is called lowering could potentially overcome this problem.[2]
On the other side, reactive programming is a form of what could be described as "explicit parallelism", and could therefore be beneficial for utilizing the power of parallel hardware.
Similarities with observer pattern
Reactive programming has principal similarities with the observer pattern commonly used in object-oriented programming. However, integrating the data flow concepts into the programming language would make it easier to express them, and could therefore increase the granularity of the data flow graph. For example, the observer pattern commonly describes data-flows between whole objects/classes, whereas object-oriented reactive programming could target the members of objects/classes.
The stack-based evaluation model of common object orientation is also not entirely suitable for data-flow propagation, as occurrences of "tree feedback edges" in the data structures could make the program face exponential complexities. But because of its relatively limited use and low granularity, this is rarely a problem for the observer pattern in practice.
Approaches
Imperative
It is possible to fuse reactive programming with ordinary imperative programming. In such a paradigm, imperative programs operate upon reactive data structures.[3] Such a set-up is analogous to constraint imperative programming; however, while constraint imperative programming manages bidirectional constraints, reactive imperative programming manages one-way dataflow constraints.
Object-oriented
Object-oriented reactive programming (OORP) is a combination of object oriented programming and reactive programming. Perhaps the most natural way to make such a combination is as follows: Instead of methods and fields, objects have reactions that automatically re-evaluate when the other reactions they depend on have been modified. Below is an illustration of the A=X+Y introductory example:[4]
function setA() { // A=X+Y as integers
var A = parseInt($('#X').text()) + parseInt($('#Y').text());
$('#A').text(A);
}
setA(); // for initial value of A
$('#X,#Y').css('cursor', 'pointer').click(function () {
// by reaction to a click at X or at Y...
var obj = $(this);
obj.text(parseInt(obj.text()) + 1); // updates X or Y
setA(); // updates A
});
If an OORP programming language maintains its imperative methods, it would also fall under the category of imperative reactive programming.
Functional
Functional reactive programming (FRP) is a programming paradigm for reactive programming on functional programming.
See also
- Service Component Architecture
- Meteor (web framework)
- QML
- Elm (programming language) Reactive composition of web user interface.
- RxJS, the Reactive Extensions library for "composing asynchronous [...] programs using observable sequences"
- ProAct.js, a powerful Reactive Programming JavaScript library, integrating both the functional and object-oriented implementation approaches.
- React, a JavaScript library written by Facebook for creating user interfaces.
- Shiny, a web application framework for R (programming language) based on reactive programming.
References
- ↑ Trellis, Model-view-controller and the observer pattern, Tele community.
- ↑ Burchett, Kimberley; Cooper, Gregory H; Krishnamurthi, Shriram, "Lowering: a static optimization technique for transparent functional reactivity", Proceedings of the 2007 ACM SIGPLAN symposium on Partial evaluation and semantics-based program manipulation (PDF), pp. 71–80.
- ↑ Demetrescu, Camil; Finocchi, Irene; Ribichini, Andrea, "Reactive Imperative Programming with Dataflow Constraints", Proceedings of the 2011 ACM international conference on Object oriented programming systems languages and applications, pp. 407–26.
- ↑ example of A=X+Y (jQuery), JS fiddle.
External links
- Meteor.js A full-stack, JavaScript-based, reactive web application development platform.
- A survey on reactive programming A paper by E. Bainomugisha, A. Lombide Carreton, T. Van Cutsem, S. Mostinckx, and W. De Meuter that surveys and provides a taxonomy of existing reactive programming approaches.
- MIMOSA Project of INRIA - ENSMP, a general site about reactive programming.
- Experimenting with Cells Demonstration of a simple reactive programming application in Lisp, using the Cells library
- REScala Reactive programming for OO applications.
- Reactive Programming in .NET Microsoft's Reactive Extensions (Rx) homepage
- Reactive Extensions for Swift RxSwift homepage
- Deprecating the Observer Pattern A 2010 paper by Ingo Maier, Tiark Rompf and Martin Odersky outlining a reactive programming framework for the Scala programming language.
- Deprecating the Observer Pattern with Scala.React A 2012 paper by Ingo Maier and Martin Odersky.
- The Reactive Manifesto
- Reactive Collections