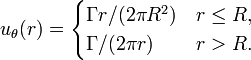Rankine vortex

The Rankine vortex is a type of vortex in a viscous fluid. It is named after its discoverer, William John Macquorn Rankine.

A swirling flow in a viscous fluid can be characterized by a forced vortex in its central core, surrounded by a free vortex. In an inviscid fluid, on the other hand, a swirling flow consists entirely of the free vortex with a singularity at its center point instead of the forced vortex core. The tangential velocity[1] of a Rankine vortex with circulation 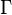\Gamma and radius R is

u_\theta(r) = \begin{cases} \Gamma r/(2 \pi R^2) & r \le R, \\ \Gamma/(2 \pi r) & r > R. \end{cases}

The remainder of the velocity components are identically zero, so that the total velocity field is 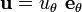\mathbf{u} = u_\theta\ \mathbf{e_\theta}.

See also

External links

Notes

  1. ↑ D. J. Acheson (1990). Elementary Fluid Dynamics. Oxford University Press. ISBN 0-19-859679-0.
This article is issued from Wikipedia - version of the Sunday, November 09, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.