Random structure function

The random structure function^[1] is the third component of the Bernoulli space which constitutes the stochastic model within Bernoulli stochastics.^[2] The Bernoulli space describes the transition from past to future. The determinate past is represented by a variable D which is called deterministic variable, because its value is fixed. The future represented by the variable X is subject to randomness and X is therefore called random variable. The random variable X may adopt one of a set of different values according to a random law which depends on the actual initial conditions given by the value d of the deterministic variable. The random law does not only fix the range of variability of X but also the probability of the future events which are given by subsets of the range of variability of X.

Probability distribution

The random variable X stands for the future indeterminate outcome of a process. If the process is repeated then different outcomes will occur according to a random law that depends on the actual initial conditions given by the value d of the deterministic variable D. The random variable X under the condition d is denoted $X|\{d\}$ where the set of possible initial conditions is given by the ignorance space $\mathfrak{D}$ . The random structure function assigns to each subset of the ignorance space a probability distribution.

Let 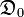$\mathfrak{D}_0$ be a subset of the ignorance space 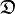$\mathfrak{D}$ then the corresponding probability distribution is obtained from the images 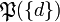$\mathfrak{P}(\{d\})$ of the singletons 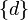$\{d\}$ as follows:

\mathfrak{P}(\mathfrak{D}_0)) = \frac{1}{|\mathfrak{D}_0|} \sum_{d \in \mathfrak{D}_0}\mathfrak{P}(\{d\})

It follows that for any future event E, we have:

P_{X|\mathfrak{D}_0}(E) = \frac{1}{|\mathfrak{D}_0|} \sum_{d \in \mathfrak{D}_0} P_{X|\{d\}}(E)

Thus, the probability distribution of the random variable 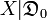$X|\mathfrak{D}_0$ is given by the mean of the probability distributions of the random variables $X|\{d_0\}$ .

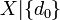References

↑ Elart von Collani, Defining and Modeling Uncertainty, Journal of Uncertainty Systems, Vol. 2, 202−211, 2008, .
↑ Elart von Collani (ed.), Defining the Science Stochastics, Heldermann Verlag, Lemgo, 2004.

External links

Stochastikon Ecyclopedia,
E-Learning Programme Stochastikon Magister,
Homepage of Stochastikon GmbH,
Economic Quality Control,

This article is issued from Wikipedia - version of the Friday, January 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.