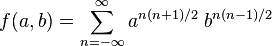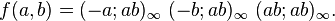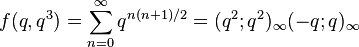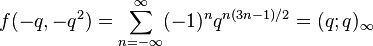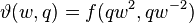Ramanujan theta function

This is not about the mock theta functions discovered by Ramanujan.

In mathematics, particularly q-analog theory, the Ramanujan theta function generalizes the form of the Jacobi theta functions, while capturing their general properties. In particular, the Jacobi triple product takes on a particularly elegant form when written in terms of the Ramanujan theta. The function is named after Srinivasa Ramanujan.

Definition

The Ramanujan theta function is defined as

f(a,b) = \sum_{n=-\infty}^\infty a^{n(n+1)/2} \; b^{n(n-1)/2}

for |ab| < 1. The Jacobi triple product identity then takes the form

f(a,b) = (-a; ab)_\infty \;(-b; ab)_\infty \;(ab;ab)_\infty.

Here, the expression $(a;q)_n$ denotes the q-Pochhammer symbol. Identities that follow from this include

f(q,q) = \sum_{n=-\infty}^\infty q^{n^2} = {(-q;q^2)_\infty^2 (q^2;q^2)_\infty}

and

f(q,q^3) = \sum_{n=0}^\infty q^{n(n+1)/2} = {(q^2;q^2)_\infty}{(-q; q)_\infty}

and

f(-q,-q^2) = \sum_{n=-\infty}^\infty (-1)^n q^{n(3n-1)/2} = (q;q)_\infty

this last being the Euler function, which is closely related to the Dedekind eta function. The Jacobi theta function may be written in terms of the Ramanujan theta function as:

\vartheta(w, q)=f(qw^2,qw^{-2})

Application in String Theory

The Ramanujan theta function is used to determine the critical dimensions in Bosonic string theory, Superstring Theory and M-theory.

References

Bailey, W. N. (1935). Generalized Hypergeometric Series. Cambridge Tracts in Mathematics and Mathematical Physics 32. Cambridge: Cambridge University Press.
Gasper, George; Rahman, Mizan (2004). Basic Hypergeometric Series. Encyclopedia of Mathematics and Its Applications 96 (2nd ed.). Cambridge: Cambridge University Press. ISBN 0-521-83357-4.
Hazewinkel, Michiel, ed. (2001), "Ramanujan function", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Kaku, Michio (1994). Hyperspace: A Scientific Odyssey Through Parallel Universes, Time Warps, and the Tenth Dimension. Oxford: Oxford University Press. ISBN 0-19-286189-1.
Weisstein, Eric W., "Ramanujan Theta Functions", MathWorld.

This article is issued from Wikipedia - version of the Thursday, June 25, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.