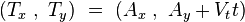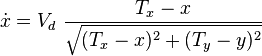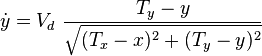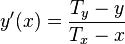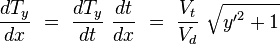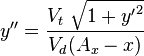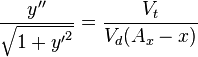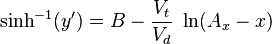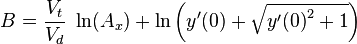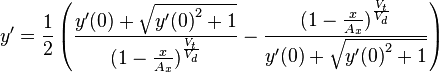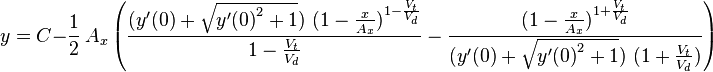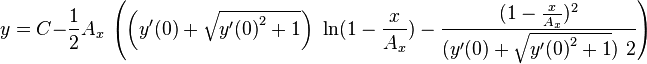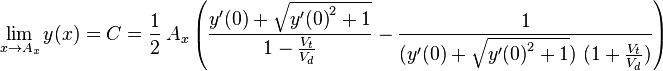Radiodrome

In geometry, a radiodrome is the pursuit curve followed by a point that is pursuing another linearly-moving point. The term is derived from the Latin word radius (beam) and the Greek word dromos (running). The classical (and best-known) form of a radiodrome is known as the "dog curve"; this is the path a dog follows when it swims across a stream with a current after food it has spotted on the other side. Because the dog drifts downwards with the current, it will have to change its heading; it will also have to swim further than if it had computed the optimal heading. This case was described by Pierre Bouguer in 1732.

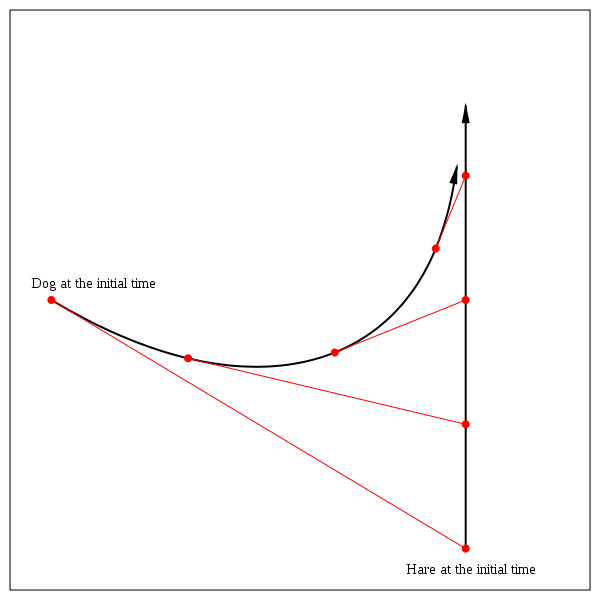
A radiodrome may alternatively be described as the path a dog follows when chasing a hare, assuming that the hare runs in a straight line at a constant velocity. It is illustrated by the following figure:

Graph of a radiodrome, also known as a dog curve

Mathematical analysis

Introduce a coordinate system with origin at the position of the dog at time zero and with y-axis in the direction the hare is running with the constant speed $V_t$ . The position of the hare at time zero is 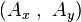$(A_x\ ,\ A_y)$ and at time $t$ it is

$(T_x\ ,\ T_y)\ =\ (A_x\ ,\ A_y+V_t t)$

(1)

The dog runs with the constant speed 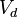$V_d$ towards the momentary position of the hare. The differential equation corresponding to the movement of the dog, 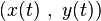$(x(t)\ ,\ y(t))$ , is consequently

$\dot x= V_d\ \frac{T_x-x}{\sqrt{(T_x-x)^2+(T_y-y)^2}}$

(2)

$\dot y= V_d\ \frac{T_y-y}{\sqrt{(T_x-x)^2+(T_y-y)^2}}$

(3)

It is possible to obtain a closed form analytical expression $y=f(x)$ for the motion of the dog

From (2) and (3) follows that

$y'(x)=\frac{T_y-y}{T_x-x}$

(4)

Multiplying both sides with 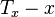$T_x-x$ and taking the derivative with respect to $x$ using that

$\frac{dT_y}{dx}\ =\ \frac{dT_y}{dt}\ \frac{dt}{dx}\ =\ \frac{V_t}{V_d}\ \sqrt{{y'}^2+1}$

(5)

one gets

$y''=\frac{V_t\ \sqrt{1+{y'}^2}}{V_d(A_x-x)}$

(6)

$\frac{y''}{\sqrt{1+{y'}^2}}=\frac{V_t}{V_d(A_x-x)}$

(7)

From this relation follows that

$\sinh^{-1}(y')=B-\frac{V_t}{V_d}\ \ln(A_x-x)$

(8)

where $B$ is the constant of integration that is determined by the initial value of $y'$ at time zero, i.e.

$B=\frac{V_t}{V_d}\ \ln(A_x)+\ln\left(y'(0)+\sqrt{{y'(0)}^2+1}\right)$

(9)

From (8) and (9) follows after some computations that

$y'= \frac{1}{2}\left(\frac{y'(0)+\sqrt{{y'(0)}^2+1}}{(1-\frac{x}{A_x})^{\frac{V_t}{V_d}}} - \frac{(1-\frac{x}{A_x})^{\frac{V_t}{V_d}}}{y'(0)+\sqrt{{y'(0)}^2+1}}\right)$

(10)

If now 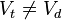$V_t \neq V_d$ this relation is integrated as

$y= C - \frac{1}{2}\ A_x\left( \frac{(y'(0)+\sqrt{{y'(0)}^2+1})\ (1-\frac{x}{A_x}) ^{1 - \frac{V_t}{V_d}} }{1-\frac{V_t}{V_d}} - \frac{ (1-\frac{x}{A_x}) ^{1 + \frac{V_t}{V_d}} }{ (y'(0)+\sqrt{{y'(0)}^2+1})\ (1 + \frac{V_t}{V_d}) } \right)$

(11)

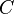where $C$ is the constant of integration.

If 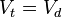$V_t = V_d$ one gets instead

$y= C -\frac{1}{2}A_x\ \left(\left(y'(0)+\sqrt{{y'(0)}^2+1}\right)\ \ln(1-\frac{x}{A_x}) - \frac{ (1-\frac{x}{A_x}) ^2}{(y'(0)+\sqrt{{y'(0)}^2+1})\ 2}\right)$

(12)

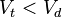If $V_t < V_d$ one gets from (11) that

$\lim_{x \to A_x}y(x) = C = \frac{1}{2}\ A_x\left( \frac{y'(0)+\sqrt{{y'(0)}^2+1} }{1-\frac{V_t}{V_d}} - \frac{1}{ (y'(0)+\sqrt{{y'(0)}^2+1})\ (1 + \frac{V_t}{V_d}) } \right)$

(13)

In the case illustrated in the figure above 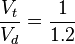$\frac{V_t}{V_d} = \frac{1}{1.2}$ and the chase starts with the hare at position 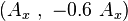$(A_x\ ,\ -0.6\ A_x)$ what means that 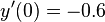$y'(0) = -0.6$ . From (13) one therefore gets that the hare is caught at position 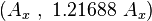$(A_x\ ,\ 1.21688\ A_x)$ and consequently that the hare will run the total distance 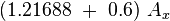$(1.21688\ +\ 0.6)\ A_x$ before being caught.

If 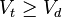$V_t \geq V_d$ one gets from (11) and (12) that 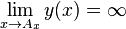$\lim_{x \to A_x}y(x) = \infty$ what means that the hare never will be caught whenever the chase starts.

Radiodrome

Mathematical analysis

See also