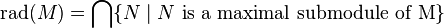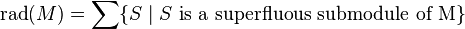Radical of a module
In mathematics, in the theory of modules, the radical of a module is a component in the theory of structure and classification. It is a generalization of the Jacobson radical for rings. In many ways, it is the dual notion to that of the socle soc(M) of M.
Definition
Let R be a ring and M a left R-module. A submodule N of M is called maximal or cosimple if the quotient M/N is a simple module. The radical of the module M is the intersection of all maximal submodules of M,
Equivalently,
These definitions have direct dual analogues for soc(M).
Properties
- In addition to the fact rad(M) is the sum of superfluous submodules, in a Noetherian module rad(M) itself is a superfluous submodule.
- A ring for which rad(M) ={0} for every right R module M is called a right V-ring.
- For any module M, rad(M/rad(M)) is zero.
- M is a finitely generated module if and only if M/rad(M) is finitely generated and rad(M) is a superfluous submodule of M.
See also
References
- Alperin, J.L.; Rowen B. Bell (1995). Groups and representations. Springer-Verlag. p. 136. ISBN 0-387-94526-1.
- Anderson, Frank Wylie; Kent R. Fuller (1992). Rings and Categories of Modules. Springer-Verlag. ISBN 978-0-387-97845-1.
This article is issued from Wikipedia - version of the Thursday, July 24, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.