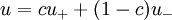Sommerfeld radiation condition

Arnold Sommerfeld defined the condition of radiation for a scalar field satisfying the Helmholtz equation as

"the sources must be sources, not sinks of energy. The energy which is radiated from the sources must scatter to infinity; no energy may be radiated from infinity into ... the field."^[1]

Mathematically, consider the inhomogeneous Helmholtz equation

(\nabla^2 + k^2) u = -f \mbox{ in } \mathbb R^n

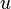where $n=2, 3$ is the dimension of the space, $f$ is a given function with compact support representing a bounded source of energy, and $k>0$ is a constant, called the wavenumber. A solution $u$ to this equation is called radiating if it satisfies the Sommerfeld radiation condition

\lim_{|x| \to \infty} |x|^{\frac{n-1}{2}} \left( \frac{\partial}{\partial |x|} - ik \right) u(x) = 0

uniformly in all directions

\hat{x} = \frac{x}{|x|}

(above, $i$ is the imaginary unit and $|\cdot|$ is the Euclidean norm). Here, it is assumed that the time-harmonic field is $e^{-i\omega t}u.$ If the time-harmonic field is instead $e^{i\omega t}u,$ one should replace $-i$ with $+i$ in the Sommerfeld radiation condition.

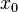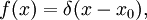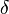The Sommerfeld radiation condition is used to solve uniquely the Helmholtz equation. For example, consider the problem of radiation due to a point source $x_0$ in three dimensions, so the function $f$ in the Helmholtz equation is $f(x)=\delta(x-x_0),$ where $\delta$ is the Dirac delta function. This problem has an infinite number of solutions, for example, any function of the form

u = cu_+ + (1-c) u_- \,

where $c$ is a constant, and

u_{\pm}(x) = \frac{e^{\pm ik|x-x_0|}}{4\pi |x-x_0|}.

Of all these solutions, only $u_+$ satisfies the Sommerfeld radiation condition and corresponds to a field radiating from $x_0.$ The other solutions are unphysical. For example, $u_{-}$ can be interpreted as energy coming from infinity and sinking at $x_0.$

References

↑ A. Sommerfeld, Partial Differential Equations in Physics, Academic Press, New York, New York, 1949.

Martin, P. A (2006). Multiple scattering: interaction of time-harmonic waves with N obstacles. Cambridge; New York: Cambridge University Press. ISBN 0-521-86554-9.
"Eighty years of Sommerfeld’s radiation condition", Steven H. Schot, Historia Mathematica 19, #4 (November 1992), pp. 385-401, doi:10.1016/0315-0860(92)90004-U.

External links

A.G. Sveshnikov (2001), "Radiation conditions", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

This article is issued from Wikipedia - version of the Thursday, November 06, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.