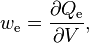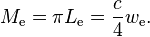Radiant energy density

In radiometry, radiant energy density is the radiant energy per unit volume.^[1] The SI unit of radiant energy density is the joule per cubic metre (J/m³).

Mathematical definition

Radiant energy density, denoted w_e ("e" for "energetic", to avoid confusion with photometric quantities), is defined as^[2]

w_{\mathrm {e} }={\frac {\partial Q_{\mathrm {e} }}{\partial V}},

where

∂ is the partial derivative symbol;
Q_e is the radiant energy;
V is the volume.

Relation to other radiometric quantities

Because radiation always transmits the energy,^[2] it is useful to wonder what the speed of the transmission is. If all the radiation at given location propagates in the same direction, then the radiant flux through a unit area perpendicular to the propagation direction is given by the irradiance:^[2]

E_{\mathrm {e} }=cw_{\mathrm {e} },

where c is the radiation propagation speed.

Contrarily if the radiation intensity is equal in all directions, like in a cavity in a thermodynamic equilibrium, then the energy transmition is best described by radiance:^[3]

L_{\mathrm {e} }={\frac {c}{4\pi }}w_{\mathrm {e} }.

Radiant exitance through a small opening from such a cavity is:^[4]

M_{\mathrm {e} }=\pi L_{\mathrm {e} }={\frac {c}{4}}w_{\mathrm {e} }.

These relations can be used for example in the black-body radiation equation's derivation.

SI radiometry units

**SI radiometry units**
Quantity		Unit		Dimension	Notes
Name	Symbol^{[nb 1]}	Name	Symbol	Symbol	Notes
Radiant energy	Q_e^{[nb 2]}	joule	J	M⋅L²⋅T⁻²	Energy of electromagnetic radiation.
Radiant energy density	w_e	joule per cubic metre	J/m³	M⋅L⁻¹⋅T⁻²	Radiant energy per unit volume.
Radiant flux	Φ_e^{[nb 2]}	watt	W or J/s	M⋅L²⋅T⁻³	Radiant energy emitted, reflected, transmitted or received, per unit time. This is sometimes also called "radiant power".
Spectral flux	Φ_e,ν^{[nb 3]} or Φ_e,λ^{[nb 4]}	watt per hertz or watt per metre	W/Hz or W/m	M⋅L²⋅T⁻² or M⋅L⋅T⁻³	Radiant flux per unit frequency or wavelength. The latter is commonly measured in W⋅sr⁻¹⋅m⁻²⋅nm⁻¹.
Radiant intensity	I_e,Ω^{[nb 5]}	watt per steradian	W/sr	M⋅L²⋅T⁻³	Radiant flux emitted, reflected, transmitted or received, per unit solid angle. This is a directional quantity.
Spectral intensity	I_e,Ω,ν^{[nb 3]} or I_e,Ω,λ^{[nb 4]}	watt per steradian per hertz or watt per steradian per metre	W⋅sr⁻¹⋅Hz⁻¹ or W⋅sr⁻¹⋅m⁻¹	M⋅L²⋅T⁻² or M⋅L⋅T⁻³	Radiant intensity per unit frequency or wavelength. The latter is commonly measured in W⋅sr⁻¹⋅m⁻²⋅nm⁻¹. This is a directional quantity.
Radiance	L_e,Ω^{[nb 5]}	watt per steradian per square metre	W⋅sr⁻¹⋅m⁻²	M⋅T⁻³	Radiant flux emitted, reflected, transmitted or received by a surface, per unit solid angle per unit projected area. This is a directional quantity. This is sometimes also confusingly called "intensity".
Spectral radiance	L_e,Ω,ν^{[nb 3]} or L_e,Ω,λ^{[nb 4]}	watt per steradian per square metre per hertz or watt per steradian per square metre, per metre	W⋅sr⁻¹⋅m⁻²⋅Hz⁻¹ or W⋅sr⁻¹⋅m⁻³	M⋅T⁻² or M⋅L⁻¹⋅T⁻³	Radiance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅sr⁻¹⋅m⁻²⋅nm⁻¹. This is a directional quantity. This is sometimes also confusingly called "spectral intensity".
Irradiance	E_e^{[nb 2]}	watt per square metre	W/m²	M⋅T⁻³	Radiant flux received by a surface per unit area. This is sometimes also confusingly called "intensity".
Spectral irradiance	E_e,ν^{[nb 3]} or E_e,λ^{[nb 4]}	watt per square metre per hertz or watt per square metre, per metre	W⋅m⁻²⋅Hz⁻¹ or W/m³	M⋅T⁻² or M⋅L⁻¹⋅T⁻³	Irradiance of a surface per unit frequency or wavelength. The terms spectral flux density or more confusingly "spectral intensity" are also used. Non-SI units of spectral irradiance include Jansky = 10⁻²⁶ W⋅m⁻²⋅Hz⁻¹ and solar flux unit (1SFU = 10⁻²² W⋅m⁻²⋅Hz⁻¹).
Radiosity	J_e^{[nb 2]}	watt per square metre	W/m²	M⋅T⁻³	Radiant flux leaving (emitted, reflected and transmitted by) a surface per unit area. This is sometimes also confusingly called "intensity".
Spectral radiosity	J_e,ν^{[nb 3]} or J_e,λ^{[nb 4]}	watt per square metre per hertz or watt per square metre, per metre	W⋅m⁻²⋅Hz⁻¹ or W/m³	M⋅T⁻² or M⋅L⁻¹⋅T⁻³	Radiosity of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m⁻²⋅nm⁻¹. This is sometimes also confusingly called "spectral intensity".
Radiant exitance	M_e^{[nb 2]}	watt per square metre	W/m²	M⋅T⁻³	Radiant flux emitted by a surface per unit area. This is the emitted component of radiosity. "Radiant emittance" is an old term for this quantity. This is sometimes also confusingly called "intensity".
Spectral exitance	M_e,ν^{[nb 3]} or M_e,λ^{[nb 4]}	watt per square metre per hertz or watt per square metre, per metre	W⋅m⁻²⋅Hz⁻¹ or W/m³	M⋅T⁻² or M⋅L⁻¹⋅T⁻³	Radiant exitance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m⁻²⋅nm⁻¹. "Spectral emittance" is an old term for this quantity. This is sometimes also confusingly called "spectral intensity".
Radiant exposure	H_e	joule per square metre	J/m²	M⋅T⁻²	Radiant energy received by a surface per unit area, or equivalently irradiance of a surface integrated over time of irradiation. This is sometimes also called "radiant fluence".
Spectral exposure	H_e,ν^{[nb 3]} or H_e,λ^{[nb 4]}	joule per square metre per hertz or joule per square metre, per metre	J⋅m⁻²⋅Hz⁻¹ or J/m³	M⋅T⁻¹ or M⋅L⁻¹⋅T⁻²	Radiant exposure of a surface per unit frequency or wavelength. The latter is commonly measured in J⋅m⁻²⋅nm⁻¹. This is sometimes also called "spectral fluence".
Hemispherical emissivity	ε			1	Radiant exitance of a surface, divided by that of a black body at the same temperature as that surface.
Spectral hemispherical emissivity	ε_ν or ε_λ			1	Spectral exitance of a surface, divided by that of a black body at the same temperature as that surface.
Directional emissivity	ε_Ω			1	Radiance emitted by a surface, divided by that emitted by a black body at the same temperature as that surface.
Spectral directional emissivity	ε_Ω,ν or ε_Ω,λ			1	Spectral radiance emitted by a surface, divided by that of a black body at the same temperature as that surface.
Hemispherical absorptance	A			1	Radiant flux absorbed by a surface, divided by that received by that surface. This should not be confused with "absorbance".
Spectral hemispherical absorptance	A_ν or A_λ			1	Spectral flux absorbed by a surface, divided by that received by that surface. This should not be confused with "spectral absorbance".
Directional absorptance	A_Ω			1	Radiance absorbed by a surface, divided by the radiance incident onto that surface. This should not be confused with "absorbance".
Spectral directional absorptance	A_Ω,ν or A_Ω,λ			1	Spectral radiance absorbed by a surface, divided by the spectral radiance incident onto that surface. This should not be confused with "spectral absorbance".
Hemispherical reflectance	R			1	Radiant flux reflected by a surface, divided by that received by that surface.
Spectral hemispherical reflectance	R_ν or R_λ			1	Spectral flux reflected by a surface, divided by that received by that surface.
Directional reflectance	R_Ω			1	Radiance reflected by a surface, divided by that received by that surface.
Spectral directional reflectance	R_Ω,ν or R_Ω,λ			1	Spectral radiance reflected by a surface, divided by that received by that surface.
Hemispherical transmittance	T			1	Radiant flux transmitted by a surface, divided by that received by that surface.
Spectral hemispherical transmittance	T_ν or T_λ			1	Spectral flux transmitted by a surface, divided by that received by that surface.
Directional transmittance	T_Ω			1	Radiance transmitted by a surface, divided by that received by that surface.
Spectral directional transmittance	T_Ω,ν or T_Ω,λ			1	Spectral radiance transmitted by a surface, divided by that received by that surface.
Hemispherical attenuation coefficient	μ	reciprocal metre	m⁻¹	L⁻¹	Radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume.
Spectral hemispherical attenuation coefficient	μ_ν or μ_λ	reciprocal metre	m⁻¹	L⁻¹	Spectral radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume.
Directional attenuation coefficient	μ_Ω	reciprocal metre	m⁻¹	L⁻¹	Radiance absorbed and scattered by a volume per unit length, divided by that received by that volume.
Spectral directional attenuation coefficient	μ_Ω,ν or μ_Ω,λ	reciprocal metre	m⁻¹	L⁻¹	Spectral radiance absorbed and scattered by a volume per unit length, divided by that received by that volume.
See also: SI · Radiometry · Photometry

↑ Standards organizations recommend that radiometric quantities should be denoted with suffix "e" (for "energetic") to avoid confusion with photometric or photon quantities.
1 2 3 4 5 Alternative symbols sometimes seen: W or E for radiant energy, P or F for radiant flux, I for irradiance, W for radiant exitance.
1 2 3 4 5 6 7 Spectral quantities given per unit frequency are denoted with suffix "ν" (Greek)—not to be confused with suffix "v" (for "visual") indicating a photometric quantity.
1 2 3 4 5 6 7 Spectral quantities given per unit wavelength are denoted with suffix "λ" (Greek).
1 2 Directional quantities are denoted with suffix "Ω" (Greek).

References

↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Radiant energy density".
1 2 3 Karel Rusňák. Přenos energie elektromagnetickým vlněním. Department of Physics, Faculty of Applied Sciences, University of West Bohemia. 2005-11. Visited 2013-10-06
↑ Max Planck. The Theory of Heat Radiation. Equation 21. 1914.
↑ Max Planck. The Theory of Heat Radiation. Equation 7. 1914.

This article is issued from Wikipedia - version of the Thursday, April 30, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.