Radial basis function network
In the field of mathematical modeling, a radial basis function network is an artificial neural network that uses radial basis functions as activation functions. The output of the network is a linear combination of radial basis functions of the inputs and neuron parameters. Radial basis function networks have many uses, including function approximation, time series prediction, classification, and system control. They were first formulated in a 1988 paper by Broomhead and Lowe, both researchers at the Royal Signals and Radar Establishment.[1][2][3]
Network architecture

 is used as input to all radial basis functions, each with different parameters. The output of the network is a linear combination of the outputs from radial basis functions.
is used as input to all radial basis functions, each with different parameters. The output of the network is a linear combination of the outputs from radial basis functions.Radial basis function (RBF) networks typically have three layers: an input layer, a hidden layer with a non-linear RBF activation function and a linear output layer. The input can be modeled as a vector of real numbers 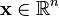 . The output of the network is then a scalar function of the input vector,
. The output of the network is then a scalar function of the input vector,  , and is given by
, and is given by
where  is the number of neurons in the hidden layer,
is the number of neurons in the hidden layer,  is the center vector for neuron
is the center vector for neuron  , and
, and  is the weight of neuron
is the weight of neuron  in the linear output neuron. Functions that depend only on the distance from a center vector are radially symmetric about that vector, hence the name radial basis function. In the basic form all inputs are connected to each hidden neuron. The norm is typically taken to be the Euclidean distance (although the Mahalanobis distance appears to perform better in general) and the radial basis function is commonly taken to be Gaussian
in the linear output neuron. Functions that depend only on the distance from a center vector are radially symmetric about that vector, hence the name radial basis function. In the basic form all inputs are connected to each hidden neuron. The norm is typically taken to be the Euclidean distance (although the Mahalanobis distance appears to perform better in general) and the radial basis function is commonly taken to be Gaussian
![\rho \big ( \left \Vert \mathbf{x} - \mathbf{c}_i \right \Vert \big ) = \exp \left[ -\beta \left \Vert \mathbf{x} - \mathbf{c}_i \right \Vert ^2 \right]](../I/m/ca850699487e278678e96a1d0da23f22.png) .
.
The Gaussian basis functions are local to the center vector in the sense that
i.e. changing parameters of one neuron has only a small effect for input values that are far away from the center of that neuron.
Given certain mild conditions on the shape of the activation function, RBF networks are universal approximators on a compact subset of 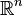 .[4] This means that an RBF network with enough hidden neurons can approximate any continuous function with arbitrary precision.
.[4] This means that an RBF network with enough hidden neurons can approximate any continuous function with arbitrary precision.
The parameters  ,
,  , and
, and  are determined in a manner that optimizes the fit between
are determined in a manner that optimizes the fit between  and the data.
and the data.

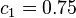 and
and 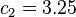 .
.
Normalized
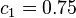 and
and 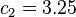 .
.
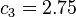

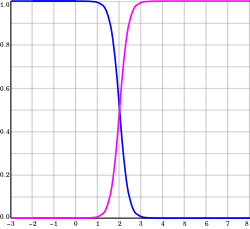
 . Note that the first basis function (dark blue) has become localized.
. Note that the first basis function (dark blue) has become localized.Normalized architecture
In addition to the above unnormalized architecture, RBF networks can be normalized. In this case the mapping is
where
is known as a "normalized radial basis function".
Theoretical motivation for normalization
There is theoretical justification for this architecture in the case of stochastic data flow. Assume a stochastic kernel approximation for the joint probability density
where the weights  and
and  are exemplars from the data and we require the kernels to be normalized
are exemplars from the data and we require the kernels to be normalized
and
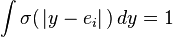 .
.
The probability densities in the input and output spaces are
and
The expectation of y given an input 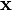 is
is
where
is the conditional probability of y given 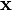 .
The conditional probability is related to the joint probability through Bayes theorem
.
The conditional probability is related to the joint probability through Bayes theorem
which yields
 .
.
This becomes
when the integrations are performed.
Local linear models
It is sometimes convenient to expand the architecture to include local linear models. In that case the architectures become, to first order,
and
in the unnormalized and normalized cases, respectively. Here 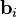 are weights to be determined. Higher order linear terms are also possible.
are weights to be determined. Higher order linear terms are also possible.
This result can be written
where
and
in the unnormalized case and
in the normalized case.
Here  is a Kronecker delta function defined as
is a Kronecker delta function defined as
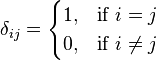 .
.
Training
RBF networks are typically trained by a two-step algorithm. In the first step, the center vectors  of the RBF functions in the hidden layer are chosen. This step can be performed in several ways; centers can be randomly sampled from some set of examples, or they can be determined using k-means clustering. Note that this step is unsupervised. A third backpropagation step can be performed to fine-tune all of the RBF net's parameters.[3]
of the RBF functions in the hidden layer are chosen. This step can be performed in several ways; centers can be randomly sampled from some set of examples, or they can be determined using k-means clustering. Note that this step is unsupervised. A third backpropagation step can be performed to fine-tune all of the RBF net's parameters.[3]
The second step simply fits a linear model with coefficients  to the hidden layer's outputs with respect to some objective function. A common objective function, at least for regression/function estimation, is the least squares function:
to the hidden layer's outputs with respect to some objective function. A common objective function, at least for regression/function estimation, is the least squares function:
where
![K_t( \mathbf{w} ) \ \stackrel{\mathrm{def}}{=}\ \big [ y(t) - \varphi \big ( \mathbf{x}(t), \mathbf{w} \big ) \big ]^2](../I/m/cabf0bf495b24628e153e69ebd5ad9ab.png) .
.
We have explicitly included the dependence on the weights. Minimization of the least squares objective function by optimal choice of weights optimizes accuracy of fit.
There are occasions in which multiple objectives, such as smoothness as well as accuracy, must be optimized. In that case it is useful to optimize a regularized objective function such as
where
and
where optimization of S maximizes smoothness and  is known as a regularization parameter.
is known as a regularization parameter.
Interpolation
RBF networks can be used to interpolate a function 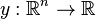 when the values of that function are known on finite number of points:
when the values of that function are known on finite number of points: 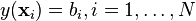 . Taking the known points
. Taking the known points  to be the centers of the radial basis functions and evaluating the values of the basis functions at the same points
to be the centers of the radial basis functions and evaluating the values of the basis functions at the same points  the weights can be solved from the equation
the weights can be solved from the equation
It can be shown that the interpolation matrix in the above equation is non-singular, if the points  are distinct, and thus the weights
are distinct, and thus the weights  can be solved by simple linear algebra:
can be solved by simple linear algebra:
Function approximation
If the purpose is not to perform strict interpolation but instead more general function approximation or classification the optimization is somewhat more complex because there is no obvious choice for the centers. The training is typically done in two phases first fixing the width and centers and then the weights. This can be justified by considering the different nature of the non-linear hidden neurons versus the linear output neuron.
Training the basis function centers
Basis function centers can be randomly sampled among the input instances or obtained by Orthogonal Least Square Learning Algorithm or found by clustering the samples and choosing the cluster means as the centers.
The RBF widths are usually all fixed to same value which is proportional to the maximum distance between the chosen centers.
Pseudoinverse solution for the linear weights
After the centers 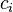 have been fixed, the weights that minimize the error at the output are computed with a linear pseudoinverse solution:
have been fixed, the weights that minimize the error at the output are computed with a linear pseudoinverse solution:
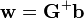 ,
,
where the entries of G are the values of the radial basis functions evaluated at the points  :
:  .
.
The existence of this linear solution means that unlike multi-layer perceptron (MLP) networks, RBF networks have a unique local minimum (when the centers are fixed).
Gradient descent training of the linear weights
Another possible training algorithm is gradient descent. In gradient descent training, the weights are adjusted at each time step by moving them in a direction opposite from the gradient of the objective function (thus allowing the minimum of the objective function to be found),
where 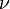 is a "learning parameter."
is a "learning parameter."
For the case of training the linear weights,  , the algorithm becomes
, the algorithm becomes
in the unnormalized case and
in the normalized case.
For local-linear-architectures gradient-descent training is
Projection operator training of the linear weights
For the case of training the linear weights,  and
and  , the algorithm becomes
, the algorithm becomes
in the unnormalized case and
in the normalized case and
in the local-linear case.
For one basis function, projection operator training reduces to Newton's method.

Examples
Logistic map
The basic properties of radial basis functions can be illustrated with a simple mathematical map, the logistic map, which maps the unit interval onto itself. It can be used to generate a convenient prototype data stream. The logistic map can be used to explore function approximation, time series prediction, and control theory. The map originated from the field of population dynamics and became the prototype for chaotic time series. The map, in the fully chaotic regime, is given by
where t is a time index. The value of x at time t+1 is a parabolic function of x at time t. This equation represents the underlying geometry of the chaotic time series generated by the logistic map.
Generation of the time series from this equation is the forward problem. The examples here illustrate the inverse problem; identification of the underlying dynamics, or fundamental equation, of the logistic map from exemplars of the time series. The goal is to find an estimate
for f.
Function approximation
Unnormalized radial basis functions
The architecture is

where
![\rho \big ( \left \Vert \mathbf{x} - \mathbf{c}_i \right \Vert \big ) = \exp \left[ -\beta \left \Vert \mathbf{x} - \mathbf{c}_i \right \Vert ^2 \right] = \exp \left[ -\beta \left ( x(t) - c_i \right ) ^2 \right]](../I/m/4c60ccf22af89bc861f37ae64f70b078.png) .
.
Since the input is a scalar rather than a vector, the input dimension is one. We choose the number of basis functions as N=5 and the size of the training set to be 100 exemplars generated by the chaotic time series. The weight 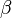 is taken to be a constant equal to 5. The weights
is taken to be a constant equal to 5. The weights 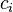 are five exemplars from the time series. The weights
are five exemplars from the time series. The weights  are trained with projection operator training:
are trained with projection operator training:
where the learning rate 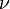 is taken to be 0.3. The training is performed with one pass through the 100 training points. The rms error is 0.15.
is taken to be 0.3. The training is performed with one pass through the 100 training points. The rms error is 0.15.

Normalized radial basis functions
The normalized RBF architecture is
where
 .
.
Again:
![\rho \big ( \left \Vert \mathbf{x} - \mathbf{c}_i \right \Vert \big ) = \exp \left[ -\beta \left \Vert \mathbf{x} - \mathbf{c}_i \right \Vert ^2 \right] = \exp \left[ -\beta \left ( x(t) - c_i \right ) ^2 \right]](../I/m/4c60ccf22af89bc861f37ae64f70b078.png) .
.
Again, we choose the number of basis functions as five and the size of the training set to be 100 exemplars generated by the chaotic time series. The weight 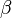 is taken to be a constant equal to 6. The weights
is taken to be a constant equal to 6. The weights 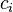 are five exemplars from the time series. The weights
are five exemplars from the time series. The weights  are trained with projection operator training:
are trained with projection operator training:
where the learning rate 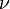 is again taken to be 0.3. The training is performed with one pass through the 100 training points. The rms error on a test set of 100 exemplars is 0.084, smaller than the unnormalized error. Normalization yields accuracy improvement. Typically accuracy with normalized basis functions increases even more over unnormalized functions as input dimensionality increases.
is again taken to be 0.3. The training is performed with one pass through the 100 training points. The rms error on a test set of 100 exemplars is 0.084, smaller than the unnormalized error. Normalization yields accuracy improvement. Typically accuracy with normalized basis functions increases even more over unnormalized functions as input dimensionality increases.

Time series prediction
Once the underlying geometry of the time series is estimated as in the previous examples, a prediction for the time series can be made by iteration:
![{x}(t+1) \approx \varphi(t)=\varphi [\varphi(t-1)]](../I/m/ef230570b4039f8a50961183a1885028.png) .
.
A comparison of the actual and estimated time series is displayed in the figure. The estimated times series starts out at time zero with an exact knowledge of x(0). It then uses the estimate of the dynamics to update the time series estimate for several time steps.
Note that the estimate is accurate for only a few time steps. This is a general characteristic of chaotic time series. This is a property of the sensitive dependence on initial conditions common to chaotic time series. A small initial error is amplified with time. A measure of the divergence of time series with nearly identical initial conditions is known as the Lyapunov exponent.
Control of a chaotic time series
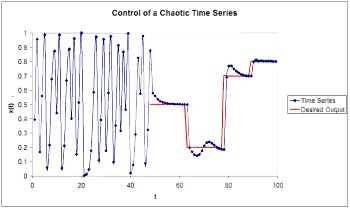
We assume the output of the logistic map can be manipulated through a control parameter ![c[ x(t),t]](../I/m/05bbd3576c59d2d858c7969d9bd15856.png) such that
such that
![{x}^{ }_{ }(t+1) = 4 x(t) [1-x(t)] +c[x(t),t]](../I/m/94deaf803d53e210470976bf835db56f.png) .
.
The goal is to choose the control parameter in such a way as to drive the time series to a desired output 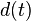 . This can be done if we choose the control paramer to be
. This can be done if we choose the control paramer to be
where
is an approximation to the underlying natural dynamics of the system.
The learning algorithm is given by
where
![\varepsilon \ \stackrel{\mathrm{def}}{=}\ f[x(t)] - \varphi [x(t)] = x(t+1)- c[x(t),t] - \varphi [x(t)] = x(t+1) - d(t+1)](../I/m/6b285bb113b9acd3d55e2f7dd4ba93b4.png) .
.
See also
References
- ↑ Broomhead, D. S.; Lowe, David (1988). Radial basis functions, multi-variable functional interpolation and adaptive networks (Technical report). RSRE. 4148.
- ↑ Broomhead, D. S.; Lowe, David (1988). "Multivariable functional interpolation and adaptive networks". Complex Systems 2: 321–355.
- 1 2 Schwenker, Friedhelm; Kestler, Hans A.; Palm, Günther (2001). "Three learning phases for radial-basis-function networks". Neural Networks 14: 439–458. doi:10.1016/s0893-6080(01)00027-2. CiteSeerX: 10
.1 ..1 .109 .312 - ↑ Park, J.; I. W. Sandberg (Summer 1991). "Universal Approximation Using Radial-Basis-Function Networks". Neural Computation 3 (2): 246–257. doi:10.1162/neco.1991.3.2.246. Retrieved 26 March 2013.
- J. Moody and C. J. Darken, "Fast learning in networks of locally tuned processing units," Neural Computation, 1, 281-294 (1989). Also see Radial basis function networks according to Moody and Darken
- T. Poggio and F. Girosi, "Networks for approximation and learning," Proc. IEEE 78(9), 1484-1487 (1990).
- Roger D. Jones, Y. C. Lee, C. W. Barnes, G. W. Flake, K. Lee, P. S. Lewis, and S. Qian, ?Function approximation and time series prediction with neural networks,? Proceedings of the International Joint Conference on Neural Networks, June 17–21, p. I-649 (1990).
- Martin D. Buhmann (2003). Radial Basis Functions: Theory and Implementations. Cambridge University. ISBN 0-521-63338-9.
- Yee, Paul V. and Haykin, Simon (2001). Regularized Radial Basis Function Networks: Theory and Applications. John Wiley. ISBN 0-471-35349-3.
- John R. Davies, Stephen V. Coggeshall, Roger D. Jones, and Daniel Schutzer, "Intelligent Security Systems," in Freedman, Roy S., Flein, Robert A., and Lederman, Jess, Editors (1995). Artificial Intelligence in the Capital Markets. Chicago: Irwin. ISBN 1-55738-811-3.
- Simon Haykin (1999). Neural Networks: A Comprehensive Foundation (2nd ed.). Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-908385-5.
- S. Chen, C. F. N. Cowan, and P. M. Grant, "Orthogonal Least Squares Learning Algorithm for Radial Basis Function Networks", IEEE Transactions on Neural Networks, Vol 2, No 2 (Mar) 1991.

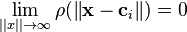
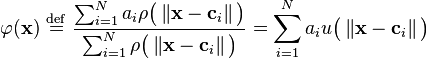
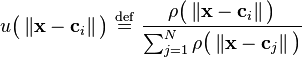
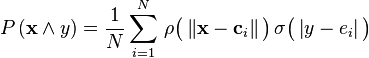

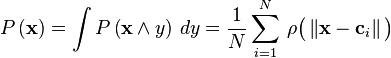
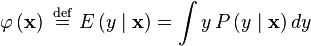
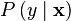
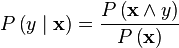
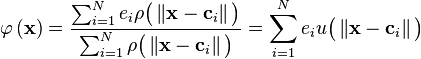


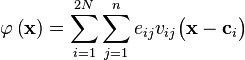
![e_{ij} = \begin{cases} a_i, & \mbox{if } i \in [1,N] \\ b_{ij}, & \mbox{if }i \in [N+1,2N] \end{cases}](../I/m/9d552af93ae3310da493d4e7133586bf.png)
![v_{ij}\big ( \mathbf{x} - \mathbf{c}_i \big ) \ \stackrel{\mathrm{def}}{=}\ \begin{cases} \delta_{ij} \rho \big ( \left \Vert \mathbf{x} - \mathbf{c}_i \right \Vert \big ) , & \mbox{if } i \in [1,N] \\ \left ( x_{ij} - c_{ij} \right ) \rho \big ( \left \Vert \mathbf{x} - \mathbf{c}_i \right \Vert \big ) , & \mbox{if }i \in [N+1,2N] \end{cases}](../I/m/d06219a032740191c0d7a35373e065f2.png)
![v_{ij}\big ( \mathbf{x} - \mathbf{c}_i \big ) \ \stackrel{\mathrm{def}}{=}\ \begin{cases} \delta_{ij} u \big ( \left \Vert \mathbf{x} - \mathbf{c}_i \right \Vert \big ) , & \mbox{if } i \in [1,N] \\ \left ( x_{ij} - c_{ij} \right ) u \big ( \left \Vert \mathbf{x} - \mathbf{c}_i \right \Vert \big ) , & \mbox{if }i \in [N+1,2N] \end{cases}](../I/m/0026388e7963b6845cfecc5c9e938aa6.png)

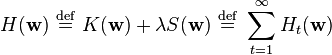
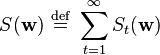
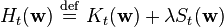
![\left[ \begin{matrix}
g_{11} & g_{12} & \cdots & g_{1N} \\
g_{21} & g_{22} & \cdots & g_{2N} \\
\vdots & & \ddots & \vdots \\
g_{N1} & g_{N2} & \cdots & g_{NN}
\end{matrix}\right] \left[ \begin{matrix}
w_1 \\
w_2 \\
\vdots \\
w_N
\end{matrix} \right] = \left[ \begin{matrix}
b_1 \\
b_2 \\
\vdots \\
b_N
\end{matrix} \right]](../I/m/6a329d7de56c97a7866e5cf0e650ba65.png)
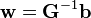

![a_i (t+1) = a_i(t) + \nu \big [ y(t) - \varphi \big ( \mathbf{x}(t), \mathbf{w} \big ) \big ] \rho \big ( \left \Vert \mathbf{x}(t) - \mathbf{c}_i \right \Vert \big )](../I/m/aad6fafed1613f5474676dcb5c633db5.png)
![a_i (t+1) = a_i(t) + \nu \big [ y(t) - \varphi \big ( \mathbf{x}(t), \mathbf{w} \big ) \big ] u \big ( \left \Vert \mathbf{x}(t) - \mathbf{c}_i \right \Vert \big )](../I/m/419021ac38cfb4f2f31bee6bb7ef9e0e.png)
![e_{ij} (t+1) = e_{ij}(t) + \nu \big [ y(t) - \varphi \big ( \mathbf{x}(t), \mathbf{w} \big ) \big ] v_{ij} \big ( \mathbf{x}(t) - \mathbf{c}_i \big )](../I/m/98d9700ab2fb374c88d7984697a8c4ad.png)
![a_i (t+1) = a_i(t) + \nu \big [ y(t) - \varphi \big ( \mathbf{x}(t), \mathbf{w} \big ) \big ] \frac {\rho \big ( \left \Vert \mathbf{x}(t) - \mathbf{c}_i \right \Vert \big )} {\sum_{i=1}^N \rho^2 \big ( \left \Vert \mathbf{x}(t) - \mathbf{c}_i \right \Vert \big )}](../I/m/95e0bdc7fb433ad19f80848c8c7080d7.png)
![a_i (t+1) = a_i(t) + \nu \big [ y(t) - \varphi \big ( \mathbf{x}(t), \mathbf{w} \big ) \big ] \frac {u \big ( \left \Vert \mathbf{x}(t) - \mathbf{c}_i \right \Vert \big )} {\sum_{i=1}^N u^2 \big ( \left \Vert \mathbf{x}(t) - \mathbf{c}_i \right \Vert \big )}](../I/m/e93a6a5c01d9cb73a01f0620b69c4c1c.png)
![e_{ij} (t+1) = e_{ij}(t) + \nu \big [ y(t) - \varphi \big ( \mathbf{x}(t), \mathbf{w} \big ) \big ] \frac { v_{ij} \big ( \mathbf{x}(t) - \mathbf{c}_i \big ) } {\sum_{i=1}^N \sum_{j=1}^n v_{ij}^2 \big ( \mathbf{x}(t) - \mathbf{c}_i \big ) }](../I/m/99991b65a1bf7eb30e102b16ec292483.png)
![x(t+1)\ \stackrel{\mathrm{def}}{=}\ f\left [ x(t)\right ] = 4 x(t) \left [ 1-x(t) \right ]](../I/m/cb29092162f637c2924e700b404f3104.png)
![x(t+1) = f \left [ x(t) \right ] \approx \varphi(t) = \varphi \left [ x(t)\right ]](../I/m/8f2f35ff674dc2314fcfa7be1cc0416b.png)

![a_i (t+1) = a_i(t) + \nu \big [ x(t+1) - \varphi \big ( \mathbf{x}(t), \mathbf{w} \big ) \big ] \frac {\rho \big ( \left \Vert \mathbf{x}(t) - \mathbf{c}_i \right \Vert \big )} {\sum_{i=1}^N \rho^2 \big ( \left \Vert \mathbf{x}(t) - \mathbf{c}_i \right \Vert \big )}](../I/m/7fa40ee2659822c9cc8d7aa41c40f24b.png)
![a_i (t+1) = a_i(t) + \nu \big [ x(t+1) - \varphi \big ( \mathbf{x}(t), \mathbf{w} \big ) \big ] \frac {u \big ( \left \Vert \mathbf{x}(t) - \mathbf{c}_i \right \Vert \big )} {\sum_{i=1}^N u^2 \big ( \left \Vert \mathbf{x}(t) - \mathbf{c}_i \right \Vert \big )}](../I/m/cc405bdc0aa3cd67bf9c6d389e6ad94b.png)
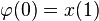
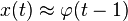
![c^{ }_{ }[x(t),t] \ \stackrel{\mathrm{def}}{=}\ -\varphi [x(t)] + d(t+1)](../I/m/9d7b2a1622bbda0acc9e95b7ceb8ec83.png)
![y[x(t)] \approx f[x(t)] = x(t+1)- c[x(t),t]](../I/m/c9ac6f37caa241d8fd033d380276ebaf.png)
