Rademacher complexity
In computational learning theory (machine learning and theory of computation), Rademacher complexity, named after Hans Rademacher, measures richness of a class of real-valued functions with respect to a probability distribution.
Given a training sample 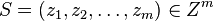 , and a class
, and a class  of real-valued functions defined on a domain space
of real-valued functions defined on a domain space 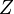 , the empirical Rademacher complexity of
, the empirical Rademacher complexity of  is defined as:
is defined as:
![\widehat{\mathcal{R}}_S(\mathcal{H})
=
\frac{2}{m}
\mathbb{E} \left[
\sup_{h \in \mathcal{H}}
\left|
\sum_{i=1}^m \sigma_i h(z_i)
\right| \ \bigg| \ S
\right]](../I/m/947f2926553a4d51058477136d9c1120.png)
where 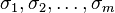 are independent random variables drawn from the Rademacher distribution i.e.
are independent random variables drawn from the Rademacher distribution i.e.
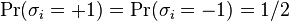 for
for 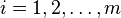 .
.
Let  be a probability distribution over
be a probability distribution over  .
The Rademacher complexity of the function class
.
The Rademacher complexity of the function class  with respect to
with respect to  for sample size
for sample size  is:
is:
![\mathcal{R}_m(\mathcal{H})
=
\mathbb{E} \left[ \widehat{\mathcal{R}}_S(\mathcal{H}) \right]](../I/m/f8d595062e1d8a9e3377177eca19de81.png)
where the above expectation is taken over an identically independently distributed (i.i.d.) sample 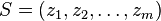 generated according to
generated according to  .
.
One can show, for example, that there exists a constant  , such that any class of
, such that any class of  -indicator functions with Vapnik-Chervonenkis dimension
-indicator functions with Vapnik-Chervonenkis dimension 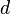 has Rademacher complexity upper-bounded by
has Rademacher complexity upper-bounded by 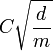 .
.
Gaussian complexity
Gaussian complexity is a similar complexity with similar physical meanings, and can be obtained from the previous complexity using the random variables 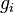 instead of
instead of  , where
, where 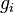 are Gaussian i.i.d. random variables with zero-mean and variance 1, i.e.
are Gaussian i.i.d. random variables with zero-mean and variance 1, i.e. 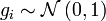 .
.
References
- Peter L. Bartlett, Shahar Mendelson (2002) Rademacher and Gaussian Complexities: Risk Bounds and Structural Results. Journal of Machine Learning Research 3 463-482
- Giorgio Gnecco, Marcello Sanguineti (2008) Approximation Error Bounds via Rademacher's Complexity. Applied Mathematical Sciences, Vol. 2, 2008, no. 4, 153 - 176