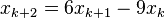RANDU

Three-dimensional plot of 100,000 values generated with RANDU. Each point represents 3 consecutive pseudorandom values. It is clearly seen that the points fall in 15 two-dimensional planes.

RANDU is a linear congruential pseudorandom number generator of the Park–Miller type, which has been used since the 1960s.^[1] It is defined by the recurrence:

V_{j+1} = 65539\cdot V_j\, \bmod\, 2^{31}\,

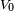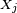with the initial seed number, $\scriptstyle V_0$ as an odd number. It generates pseudorandom integers $\scriptstyle V_j$ which are uniformly distributed in the interval [1, 2³¹ − 1], but in practical applications are often mapped into pseudorandom rationals $\scriptstyle X_j$ in the interval (0, 1), by the formula:

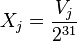X_j = \frac{V_{j}}{2^{31}}

RANDU fails the spectral test badly for dimensions greater than 2, and every integer result is odd. However, at least eight low-order bits are dropped when converted to single-precision floating-point.

The reason for choosing these particular values is that with a 32-bit-integer word size, the arithmetic of mod 2³¹ and 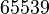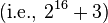$65539$ $(\text{i.e., }2^{16} + 3)$ calculations could be done quickly, using special features of some computer hardware.

Problems with multiplier and modulus

To show the problem with these values, of multiplier 65539 and modulus 2³¹, consider the following calculation where every term should be taken mod 2³¹. Start by writing the recursive relation as:

x_{k+2}=(2^{16}+3) x_{k+1}=(2^{16}+3 )^2 x_{k}\,

which becomes, after expanding the quadratic factor:

x_{k+2}=(2^{32}+6 \cdot2^{16} +9 )x_{k}=[6 \cdot (2^{16}+3)-9]x_{k}\,

because 2³² mod 2³¹ = 0

and allows us to show the correlation between three points as:

x_{k+2}=6x_{k+1}-9x_{k}\,

As a result of this correlation, the points in three-dimensional space (mod 2³¹) fall in 15 planes.^[2] As a result of the wide use of RANDU in the early 1970s, many results from that time are seen as suspicious.^[3]

This misbehavior was already detected in 1963^[4] on a 36-bit computer, and carefully reimplemented on the 32-bit IBM System/360.

Sample output

The start and end of the RANDU’s output period for the initial seed $\scriptstyle V_0 = 1$ is:

1, 65539, 393225, 1769499, 7077969, 26542323, …, 2141591611, 388843697, 238606867, 79531577, 477211307, 1 (sequence A096555 in OEIS)

References

↑ Entacher, Karl (June 2000). "A collection of classical pseudorandom number generators with linear structures - advanced version". Retrieved 8 August 2013.
↑ Marsaglia, George (1968). "Random Numbers Fall Mainly in the Planes". Proc. Natl. Acad. Sci. U.S.A. 61 (1): 25–28. doi:10.1073/pnas.61.1.25.
↑ Press, William H.; et al. (1992). Numerical Recipes in Fortran 77: The Art of Scientific Computing (2nd ed.). ISBN 0-521-43064-X.
↑ ref. 7 of http://portal.acm.org/citation.cfm?id=363827

External links

Wikiquote has quotations related to: RANDU

This article is issued from Wikipedia - version of the Friday, November 06, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.