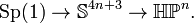Quaternionic projective space
In mathematics, quaternionic projective space is an extension of the ideas of real projective space and complex projective space, to the case where coordinates lie in the ring of quaternions H. Quaternionic projective space of dimension n is usually denoted by
and is a closed manifold of (real) dimension 4n. It is a homogeneous space for a Lie group action, in more than one way.
In coordinates
Its direct construction is as a special case of the projective space over a division algebra. The homogeneous coordinates of a point can be written
where the  are quaternions, not all zero. Two sets of coordinates represent the same point if they are 'proportional' by a left multiplication by a non-zero quaternion c; that is, we identify all the
are quaternions, not all zero. Two sets of coordinates represent the same point if they are 'proportional' by a left multiplication by a non-zero quaternion c; that is, we identify all the
![[cq_0,cq_1\ldots,cq_n]](../I/m/af3e5b6382c2f93760e5455dbceeca84.png) .
.
In the language of group actions, 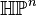 is the orbit space of
is the orbit space of 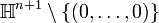 by the action of
by the action of 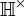 , the multiplicative group of non-zero quaternions. By first projecting onto the unit sphere inside
, the multiplicative group of non-zero quaternions. By first projecting onto the unit sphere inside 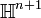 one may also regard
one may also regard 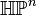 as the orbit space of
as the orbit space of 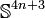 by the action of
by the action of 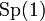 , the group of unit quaternions.[1] The sphere
, the group of unit quaternions.[1] The sphere 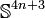 then becomes a principal Sp(1)-bundle over
then becomes a principal Sp(1)-bundle over 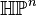 :
:
There is also a construction of 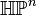 by means of two-dimensional complex subspaces of
by means of two-dimensional complex subspaces of 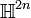 , meaning that
, meaning that 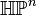 lies inside a complex Grassmannian.
lies inside a complex Grassmannian.
Projective line
The one-dimensional projective space over H is called the "projective line" in generalization of the complex projective line. For example, it was used (implicitly) in 1947 by P. G. Gormley to extend the Möbius group to the quaternion context with "linear fractional transformations". For the linear fractional transformations of an associative ring with 1, see projective line over a ring and the homography group GL(2,A).
From the topological point of view the quaternionic projective line is the 4-sphere, and in fact these are diffeomorphic manifolds. The fibration mentioned previously is from the 7-sphere, and is an example of a Hopf fibration.
Infinite-dimensional quaternionic projective space
The space 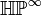 is the classifying space BS3. The homotopy groups of
is the classifying space BS3. The homotopy groups of 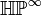 are given by
are given by 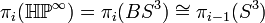 . These groups are known to be very complex and in particular they are non-zero for infinitely many values of
. These groups are known to be very complex and in particular they are non-zero for infinitely many values of  . However, we do have that
. However, we do have that 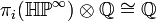 if
if 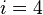 and
and 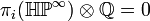 if
if 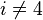 . It follows that rationally, i.e. after localisation of a space,
. It follows that rationally, i.e. after localisation of a space, 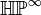 is an Eilenberg–Maclane space
is an Eilenberg–Maclane space 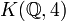 . That is
. That is 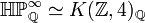 . (cf. the example K(Z,2)). See rational homotopy theory.
. (cf. the example K(Z,2)). See rational homotopy theory.
Quaternionic projective plane
The 8-dimensional 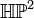 has a circle action, by the group of complex scalars of absolute value 1 acting on the other side (so on the right, as the convention for the action of c above is on the left). Therefore the quotient manifold
has a circle action, by the group of complex scalars of absolute value 1 acting on the other side (so on the right, as the convention for the action of c above is on the left). Therefore the quotient manifold
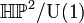
may be taken, writing U(1) for the circle group. It has been shown that this quotient is the 7-sphere, a result of Vladimir Arnold from 1996, later rediscovered by Edward Witten and Michael Atiyah.
References
- ↑ Gregory L. Naber, Topology, geometry, and gauge fields: foundations (1997), p. 50.
Further reading
- V. I. Arnol'd, Relatives of the Quotient of the Complex Projective Plane by the Complex Conjugation, Tr. Mat. Inst. Steklova, 1999, Volume 224, Pages 56–67. Treats the analogue of the result mentioned for quaternionic projective space and the 13-sphere.
![[q_0,q_1,\ldots,q_n]](../I/m/24f25cca7f1acf246c6ab30bd2080189.png)