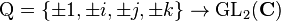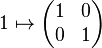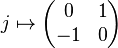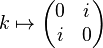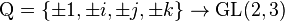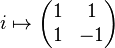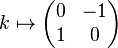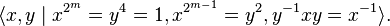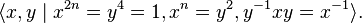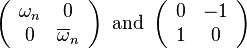Quaternion group

In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication. It is often denoted by Q or Q8, and is given by the group presentation
where 1 is the identity element and −1 commutes with the other elements of the group.
Compared to dihedral group
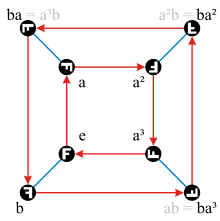
The Q8 group has the same order as the dihedral group D4, but a different structure, as shown by their Cayley and cycle graphs:
| Cayley graph | Cycle graphs | ||
|---|---|---|---|
 Q8 The red arrows represent multiplication on the right by i, and the green arrows represent multiplication on the right by j. |
 Dih4 Dihedral group |
 Q8 |
 Dih4 |
The dihedral group D4 arises in the split-quaternions in the same way that Q8 lies in the quaternions.
Cayley table
The Cayley table (multiplication table) for Q is given by:[1]
| Q×Q | 1 | −1 | i | −i | j | −j | k | −k |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | −1 | i | −i | j | −j | k | −k |
| −1 | −1 | 1 | −i | i | −j | j | −k | k |
| i | i | −i | −1 | 1 | k | −k | −j | j |
| −i | −i | i | 1 | −1 | −k | k | j | −j |
| j | j | −j | −k | k | −1 | 1 | i | −i |
| −j | −j | j | k | −k | 1 | −1 | −i | i |
| k | k | −k | j | −j | −i | i | −1 | 1 |
| −k | −k | k | −j | j | i | −i | 1 | −1 |
The multiplication of the six imaginary units {±i, ±j, ±k} works like the cross product of unit vectors in three-dimensional Euclidean space.
Properties
The quaternion group has the unusual property of being Hamiltonian: every subgroup of Q is a normal subgroup, but the group is non-abelian.[2] Every Hamiltonian group contains a copy of Q.[3]
In abstract algebra, one can construct a real four-dimensional vector space with basis {1, i, j, k} and turn it into an associative algebra by using the above multiplication table and distributivity. The result is a skew field called the quaternions. Note that this is not quite the same as the group algebra on Q (which would be eight-dimensional). Conversely, one can start with the quaternions and define the quaternion group as the multiplicative subgroup consisting of the eight elements {1, −1, i, −i, j, −j, k, −k}. The complex four-dimensional vector space on the same basis is called the algebra of biquaternions.
Note that i, j, and k all have order four in Q and any two of them generate the entire group. Another presentation of Q[4] demonstrating this is:
One may take, for instance, i = x, j = y and k = x y.
The center and the commutator subgroup of Q is the subgroup {±1}. The factor group Q/{±1} is isomorphic to the Klein four-group V. The inner automorphism group of Q is isomorphic to Q modulo its center, and is therefore also isomorphic to the Klein four-group. The full automorphism group of Q is isomorphic to S4, the symmetric group on four letters. The outer automorphism group of Q is then S4/V which is isomorphic to S3.
Matrix representations
The quaternion group can be represented as a subgroup of the general linear group GL2(C). A representation
is given by
Since all of the above matrices have unit determinant, this is a representation of Q in the special linear group SL2(C). The standard identities for quaternion multiplication can be verified using the usual laws of matrix multiplication in GL2(C).[5]
.svg.png)
There is also an important action of Q on the eight nonzero elements of the 2-dimensional vector space over the finite field F3. A representation
is given by
where {−1,0,1} are the three elements of F3. Since all of the above matrices have unit determinant over F3, this is a representation of Q in the special linear group SL(2, 3). Indeed, the group SL(2, 3) has order 24, and Q is a normal subgroup of SL(2, 3) of index 3.
Galois group
As Richard Dean showed in 1981, the quaternion group can be presented as the Galois group Gal(T/Q) where Q is the field of rational numbers and T is the splitting field, over Q, of the polynomial
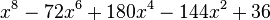 .
.
The development uses the fundamental theorem of Galois theory in specifying four intermediate fields between Q and T and their Galois groups, as well as two theorems on cyclic extension of degree four over a field.[6]
Generalized quaternion group
A group is called a generalized quaternion group[7] when its order is a power of 2 and it is dicyclic group.
It is a part of more general class of dicyclic groups.
Some authors define [4] generalized quaternion group to be the same as dicyclic group.
for some integer n ≥ 2. This group is denoted Q4n and has order 4n.[8] Coxeter labels these dicyclic groups <2,2,n>, being a special case of the binary polyhedral group <l,m,n> and related to the polyhedral groups (p,q,r), and dihedral group (2,2,n). The usual quaternion group corresponds to the case n = 2. The generalized quaternion group can be realized as the subgroup of GL2(C) generated by
where ωn = eiπ/n.[4] It can also be realized as the subgroup of unit quaternions generated by[9] x = eiπ/n and y = j.
The generalized quaternion groups have the property that every abelian subgroup is cyclic.[10] It can be shown that a finite p-group with this property (every abelian subgroup is cyclic) is either cyclic or a generalized quaternion group as defined above.[11] Another characterization is that a finite p-group in which there is a unique subgroup of order p is either cyclic or a 2-group isomorphic to generalized quaternion group.[12] In particular, for a finite field F with odd characteristic, the 2-Sylow subgroup of SL2(F) is non-abelian and has only one subgroup of order 2, so this 2-Sylow subgroup must be a generalized quaternion group, (Gorenstein 1980, p. 42). Letting pr be the size of F, where p is prime, the size of the 2-Sylow subgroup of SL2(F) is 2n, where n = ord2(p2 − 1) + ord2(r).
The Brauer–Suzuki theorem shows that groups whose Sylow 2-subgroups are generalized quaternion cannot be simple.
See also
- binary tetrahedral group
- Clifford algebra
- dicyclic group
- Hurwitz integral quaternion
- List of small groups
- 16-cell
Notes
- ↑ See also a table from Wolfram Alpha
- ↑ See Hall (1999), p. 190
- ↑ See Kurosh (1979), p. 67
- 1 2 3 Johnson 1980, pp. 44–45
- ↑ Artin 1991
- ↑ Dean, Richard (1981). "A Rational Polynomial whose Group is the Quaternions". The American Mathematical Monthly 88 (1): 42–45. JSTOR 2320711.
- ↑ Roman, Steven (2011). Fundamentals of Group Theory: An Advanced Approach. Springer. pp. 347–348. ISBN 9780817683016.
- ↑ Some authors (e.g., Rotman 1995, pp. 87, 351) refer to this group as the dicyclic group, reserving the name generalized quaternion group to the case where n is a power of 2.
- ↑ Brown 1982, p. 98
- ↑ Brown 1982, p. 101, exercise 1
- ↑ Cartan & Eilenberg 1999, Theorem 11.6, p. 262
- ↑ Brown 1982, Theorem 4.3, p. 99
References
- Artin, Michael (1991), Algebra, Prentice Hall, ISBN 978-0-13-004763-2
- Brown, Kenneth S. (1982), Cohomology of groups (3 ed.), Springer-Verlag, ISBN 978-0-387-90688-1
- Cartan, Henri; Eilenberg, Samuel (1999), Homological Algebra, Princeton University Press, ISBN 978-0-691-04991-5
- Coxeter, H. S. M. and Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9.
- Dean, Richard A. (1981) "A rational polynomial whose group is the quaternions", American Mathematical Monthly 88:42–5.
- Gorenstein, D. (1980), Finite Groups, New York: Chelsea, ISBN 978-0-8284-0301-6, MR 81b:20002
- Johnson, David L. (1980), Topics in the theory of group presentations, Cambridge University Press, ISBN 978-0-521-23108-4, MR 0695161
- Rotman, Joseph J. (1995), An introduction to the theory of groups (4 ed.), Springer-Verlag, ISBN 978-0-387-94285-8
- P.R. Girard (1984) "The quaternion group and modern physics", European Journal of Physics 5:25–32.
- Hall, Marshall (1999), The theory of groups (2 ed.), AMS Bookstore, ISBN 0-8218-1967-4
- Kurosh, Alexander G. (1979), Theory of Groups, AMS Bookstore, ISBN 0-8284-0107-1
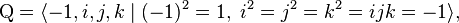
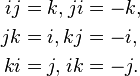
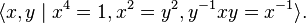
.svg.png)