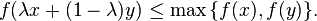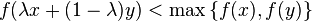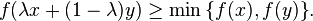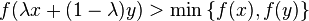Quasiconvex function

A quasiconvex function that is not convex.

A function that is not quasiconvex: the set of points in the domain of the function for which the function values are below the dashed red line is the union of the two red intervals, which is not a convex set.

The probability density function of the normal distribution is quasiconcave but not concave.

In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form $(-\infty,a)$ is a convex set. Informally, along any stretch of the curve the highest point is one of the endpoints. The negative of a quasiconvex function is said to be quasiconcave.

All convex functions are also quasiconvex, but not all quasiconvex functions are convex, so quasiconvexity is a generalization of convexity. Quasiconvexity and quasiconcavity extend to functions with multiple arguments the notion of unimodality of functions with a single real argument.

Definition and properties

A function 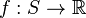$f:S \to \mathbb{R}$ defined on a convex subset S of a real vector space is quasiconvex if for all 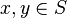$x, y \in S$ and $\lambda \in [0,1]$ we have

f(\lambda x + (1 - \lambda)y)\leq\max\big\{f(x),f(y)\big\}.

In words, if f is such that it is always true that a point directly between two other points does not give a higher value of the function than both of the other points do, then f is quasiconvex. Note that the points x and y, and the point directly between them, can be points on a line or more generally points in n-dimensional space.

A quasilinear function is both quasiconvex and quasiconcave.

The graph of a function that is both concave and quasi-convex on the nonnegative real numbers.

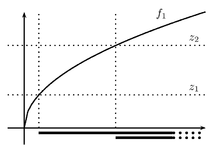
An alternative way (see introduction) of defining a quasi-convex function 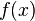$f(x)$ is to require that each sub-levelset 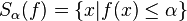$S_\alpha(f) = \{x|f(x) \leq \alpha\}$ is a convex set.

If furthermore

f(\lambda x + (1 - \lambda)y)<\max\big\{f(x),f(y)\big\}

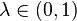for all $x \neq y$ and $\lambda \in (0,1)$ , then $f$ is strictly quasiconvex. That is, strict quasiconvexity requires that a point directly between two other points must give a lower value of the function than one of the other points does.

A quasiconcave function is a function whose negative is quasiconvex, and a strictly quasiconcave function is a function whose negative is strictly quasiconvex. Equivalently a function $f$ is quasiconcave if

f(\lambda x + (1 - \lambda)y)\geq\min\big\{f(x),f(y)\big\}.

and strictly quasiconcave if

f(\lambda x + (1 - \lambda)y)>\min\big\{f(x),f(y)\big\}

A (strictly) quasiconvex function has (strictly) convex lower contour sets, while a (strictly) quasiconcave function has (strictly) convex upper contour sets.

A function that is both quasiconvex and quasiconcave is quasilinear.

A particular case of quasi-concavity, if 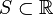$S \subset \mathbb{R}$ , is unimodality, in which there is a locally maximal value.

Applications

Quasiconvex functions have applications in mathematical analysis, in mathematical optimization, and in game theory and economics.

Mathematical optimization

In nonlinear optimization, quasiconvex programming studies iterative methods that converge to a minimum (if one exists) for quasiconvex functions. Quasiconvex programming is a generalization of convex programming.^[1] Quasiconvex programming is used in the solution of "surrogate" dual problems, whose biduals provide quasiconvex closures of the primal problem, which therefore provide tighter bounds than do the convex closures provided by Lagrangian dual problems.^[2] In theory, quasiconvex programming and convex programming problems can be solved in reasonable amount of time, where the number of iterations grows like a polynomial in the dimension of the problem (and in the reciprocal of the approximation error tolerated);^[3] however, such theoretically "efficient" methods use "divergent-series" stepsize rules, which were first developed for classical subgradient methods. Classical subgradient methods using divergent-series rules are much slower than modern methods of convex minimization, such as subgradient projection methods, bundle methods of descent, and nonsmooth filter methods.

Economics and partial differential equations: Minimax theorems

In microeconomics, quasiconcave utility functions imply that consumers have convex preferences. Quasiconvex functions are important also in game theory, industrial organization, and general equilibrium theory, particularly for applications of Sion's minimax theorem. Generalizing a minimax theorem of John von Neumann, Sion's theorem is also used in the theory of partial differential equations.

Preservation of quasiconvexity

Operations preserving quasiconvexity

non-negative weighted maximum of quasiconvex functions (i.e. 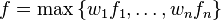$f = \max \left\lbrace w_1 f_1 , \ldots , w_n f_n \right\rbrace$ with $w_i$ non-negative)
composition with a non-decreasing function (i.e. 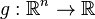$g : \mathbb{R}^{n} \rightarrow \mathbb{R}$ quasiconvex, 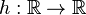$h : \mathbb{R} \rightarrow \mathbb{R}$ non-decreasing, then 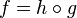$f = h \circ g$ is quasiconvex)
minimization (i.e. 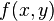$f(x,y)$ quasiconvex, 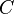$C$ convex set, then 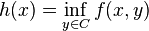$h(x) = \inf_{y \in C} f(x,y)$ is quasiconvex)

Operations not preserving quasiconvexity

The sum of quasiconvex functions defined on the same domain need not be quasiconvex: In other words, if 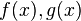$f(x), g(x)$ are quasiconvex, then 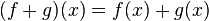$(f+g)(x) = f(x) + g(x)$ need not be quasiconvex.
The sum of quasiconvex functions defined on different domains (i.e. if 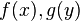$f(x), g(y)$ are quasiconvex, 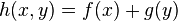$h(x,y) = f(x) + g(y)$ ) need not be quasiconvex. Such functions are called "additively decomposed" in economics and "separable" in mathematical optimization.

Examples

Every convex function is quasiconvex.
A concave function can be quasiconvex function. For example $x \mapsto \log(x)$ is concave, and it is quasiconvex.
Any monotonic function is both quasiconvex and quasiconcave. More generally, a function which decreases up to a point and increases from that point on is quasiconvex (compare unimodality).
The floor function 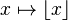$x\mapsto \lfloor x\rfloor$ is an example of a quasiconvex function that is neither convex nor continuous.
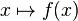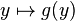If $x \mapsto f(x)$ and $y \mapsto g(y)$ are positive convex decreasing functions, then 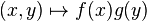$(x,y) \mapsto f(x)g(y)$ is quasiconvex.

References

↑ Di Guglielmo (1977, pp. 287–288): Di Guglielmo, F. (1977). "Nonconvex duality in multiobjective optimization". Mathematics of Operations Research 2 (3): 285–291. doi:10.1287/moor.2.3.285. JSTOR 3689518. MR 484418.
↑ Di Guglielmo, F. (1981). "Estimates of the duality gap for discrete and quasiconvex optimization problems". In Schaible, Siegfried; Ziemba, William T. Generalized concavity in optimization and economics: Proceedings of the NATO Advanced Study Institute held at the University of British Columbia, Vancouver, B.C., August 4–15, 1980. New York: Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers]. pp. 281–298. ISBN 0-12-621120-5. MR 652702.
↑ Kiwiel, Krzysztof C. (2001). "Convergence and efficiency of subgradient methods for quasiconvex minimization". Mathematical Programming (Series A) 90 (1) (Berlin, Heidelberg: Springer). pp. 1–25. doi:10.1007/PL00011414. ISSN 0025-5610. MR 1819784. Kiwiel acknowledges that Yuri Nesterov first established that quasiconvex minimization problems can be solved efficiently.

Avriel, M., Diewert, W.E., Schaible, S. and Zang, I., Generalized Concavity, Plenum Press, 1988.
Crouzeix, J.-P. (2008). "Quasi-concavity". In Durlauf, Steven N.; Blume, Lawrence E. The New Palgrave Dictionary of Economics (Second ed.). Palgrave Macmillan. doi:10.1057/9780230226203.1375.
Singer, Ivan Abstract convex analysis. Canadian Mathematical Society Series of Monographs and Advanced Texts. A Wiley-Interscience Publication. John Wiley & Sons, Inc., New York, 1997. xxii+491 pp. ISBN 0-471-16015-6

External links

SION, M., "On general minimax theorems", Pacific J. Math. 8 (1958), 171-176.
Mathematical programming glossary
Concave and Quasi-Concave Functions - by Charles Wilson, NYU Department of Economics
Quasiconcavity and quasiconvexity - by Martin J. Osborne, University of Toronto Department of Economics

This article is issued from Wikipedia - version of the Tuesday, December 01, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.