Quasi Fermi level
A quasi Fermi level (also called imref, which is "fermi" spelled backwards) is a term used in quantum mechanics and especially in solid state physics for the Fermi level (chemical potential of electrons) that describes the population of electrons separately in the conduction band and valence band, when their populations are displaced from equilibrium. This displacement could be caused by the application of an external voltage, or by exposure to light of energy 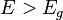 , which alter the populations of electrons in the conduction band and valence band. Since recombination rate (the rate of equilibration between bands) tends to be much slower than the energy relaxation rate within each band, the conduction band and valence band can each have an individual population that is internally in equilibrium, even though the bands are not in equilibrium with respect to exchange of electrons. The displacement from equilibrium is such that the carrier populations can no longer be described by a single Fermi level, however it is possible to describe using separate quasi-Fermi levels for each band.
, which alter the populations of electrons in the conduction band and valence band. Since recombination rate (the rate of equilibration between bands) tends to be much slower than the energy relaxation rate within each band, the conduction band and valence band can each have an individual population that is internally in equilibrium, even though the bands are not in equilibrium with respect to exchange of electrons. The displacement from equilibrium is such that the carrier populations can no longer be described by a single Fermi level, however it is possible to describe using separate quasi-Fermi levels for each band.
Definition
When a semiconductor is in thermal equilibrium, the distribution function of the electrons at the energy level of E is presented by Fermi–Dirac distribution function. In this case the Fermi level is defined as the level in which the probability of occupation of electron at that energy is 1/2. In thermal equilibrium, there is no need to distinguish between conduction band quasi-Fermi level and valence band quasi-Fermi level as they are simply equal to the Fermi level.

When a disturbance from a thermal equilibrium situation occurs, the populations of the electrons in the conduction band and valence band change. If the disturbance is not too great or not changing too quickly, the bands each relax to a state of quasi thermal equilibrium. Because the relaxation time for electrons within the conduction band is much lower than across the band gap, we can consider that the electrons are in thermal equilibrium in the conduction band. This is also applicable for electrons in the valence band (often understood in terms of holes). We can define a quasi Fermi level and quasi temperature due to thermal equilibrium of electrons in conduction band, and quasi Fermi level and quasi temperature for the valence band similarly.
We can state the general Fermi function for electrons in conduction band as
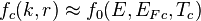
and for electrons in valence band as
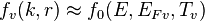
where:
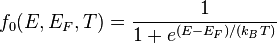 is the Fermi–Dirac distribution function,
is the Fermi–Dirac distribution function,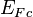 is the conduction band quasi-Fermi level at location r,
is the conduction band quasi-Fermi level at location r,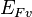 is the valence band quasi-Fermi level at location r,
is the valence band quasi-Fermi level at location r, is the conduction band temperature,
is the conduction band temperature,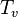 is the valence band temperature,
is the valence band temperature,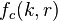 is the probability that a particular conduction-band state, with wavevector k and position r, is occupied by an electron,
is the probability that a particular conduction-band state, with wavevector k and position r, is occupied by an electron,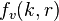 is the probability that a particular valence-band state, with wavevector k and position r, is occupied by an electron (i.e. not occupied by a hole).
is the probability that a particular valence-band state, with wavevector k and position r, is occupied by an electron (i.e. not occupied by a hole).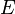 is the energy of the conduction- or valence-band state in question,
is the energy of the conduction- or valence-band state in question,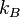 is Boltzmann's constant.
is Boltzmann's constant.
Application
This simplification will help us in many areas. For example, we can use the same equation for electron and hole densities used in thermal equilibrium, but substituting the quasi-Fermi levels and temperature. That is, if we let  be the spatial density of conduction band electrons and
be the spatial density of conduction band electrons and  be the spatial density of holes in a material, and if the Boltzmann approximation holds, i.e. assuming the electron and hole densities are not too high, then
be the spatial density of holes in a material, and if the Boltzmann approximation holds, i.e. assuming the electron and hole densities are not too high, then
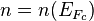
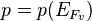
where 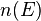 is the spatial density of conduction band electrons that would be present in thermal equilibrium if the Fermi level were at
is the spatial density of conduction band electrons that would be present in thermal equilibrium if the Fermi level were at  , and
, and 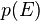 is the spatial density of holes that would be present in thermal equilibrium if the Fermi level were at
is the spatial density of holes that would be present in thermal equilibrium if the Fermi level were at 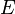 .
.
A current (due to the combined effects of drift and diffusion) will only appear if there is a variation in the Fermi or quasi Fermi level. The current density for electron flow can be shown to be proportional to the gradient in the electron quasi Fermi level. For if we let  be the electron mobility, and
be the electron mobility, and 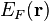 be the quasi fermi energy at the spatial point
be the quasi fermi energy at the spatial point  , then we have
, then we have
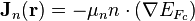 Similarly, for holes, we have
Similarly, for holes, we have
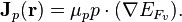
Notes
Nelson, Jenny. The Physics of Solar Cells. Imperial College Press, 2003.