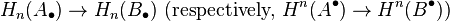Quasi-isomorphism

In homological algebra, a branch of mathematics, a quasi-isomorphism is a morphism A → B of chain complexes (respectively, cochain complexes) such that the induced morphisms

of homology groups (respectively, of cohomology groups) are isomorphisms for all n.

In the theory of model categories, quasi-isomorphisms are sometimes used as the class of weak equivalences when the objects of the category are chain or cochain complexes. This results in a homology-local theory, in the sense of Bousfield localization in homotopy theory.

See also

• Derived category

References

• Gelfand, Manin. Methods of Homological Algebra, 2nd ed. Springer, 2000.