Quasi-algebraically closed field

In mathematics, a field F is called quasi-algebraically closed (or C1) if every non-constant homogeneous polynomial P over F has a non-trivial zero provided the number of its variables is more than its degree. The idea of quasi-algebraically closed fields was investigated by C. C. Tsen, a student of Emmy Noether, in a 1936 paper (Tsen 1936); and later by Serge Lang in his 1951 Princeton University dissertation and in his 1952 paper (Lang 1952). The idea itself is attributed to Lang's advisor Emil Artin.

Formally, if P is a non-constant homogeneous polynomial in variables

X1, ..., XN,

and of degree d satisfying

d < N

then it has a non-trivial zero over F; that is, for some xi in F, not all 0, we have

P(x1, ..., xN) = 0.

In geometric language, the hypersurface defined by P, in projective space of degree N − 2, then has a point over F.

Examples

Properties

Ck fields

Quasi-algebraically closed fields are also called C1. A Ck field, more generally, is one for which any homogeneous polynomial of degree d in N variables has a non-trivial zero, provided

dk < N,

for k ≥ 1.[11] The condition was first introduced and studied by Lang.[10] If a field is Ci then so is a finite extension.[11][12] The C0 fields are precisely the algebraically closed fields.[13][14]

Lang and Nagata proved that if a field is Ck, then any extension of transcendence degree n is Ck+n.[15][16][17] The smallest k such that K is a Ck field (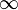\infty if no such number exists), is called the diophantine dimension dd(K) of K.[13]

C1 fields

Every finite field is C1.[7]

C2 fields

Properties

Suppose that the field k is C2.

Artin's conjecture

Artin conjectured that p-adic fields were C2, but Guy Terjanian found p-adic counterexamples for all p.[18][19] The Ax–Kochen theorem applied methods from model theory to show that Artin's conjecture was true for Qp with p large enough (depending on d).

Weakly Ck fields

A field K is weakly Ck,d if for every homogeneous polynomial of degree d in N variables satisfying

dk < N

the Zariski closed set V(f) of Pn(K) contains a subvariety which is Zariski closed over K.

A field which is weakly Ck,d for every d is weakly Ck.[2]

Properties

See also

Citations

  1. ↑ Fried & Jarden (2008) p.455
  2. 1 2 3 4 Fried & Jarden (2008) p.456
  3. 1 2 3 4 Serre (1979) p.162
  4. ↑ Gille & Szamuley (2006) p.142
  5. ↑ Gille & Szamuley (2006) p.143
  6. ↑ Gille & Szamuley (2006) p.144
  7. 1 2 Fried & Jarden (2008) p.462
  8. ↑ Lorenz (2008) p.181
  9. ↑ Serre (1979) p.161
  10. 1 2 3 Gille & Szamuely (2006) p.141
  11. 1 2 Serre (1997) p.87
  12. ↑ Lang (1997) p.245
  13. 1 2 Neukirch, Jürgen; Schmidt, Alexander; Wingberg, Kay (2008). Cohomology of Number Fields. Grundlehren der Mathematischen Wissenschaften 323 (2nd ed.). Springer-Verlag. p. 361. ISBN 3-540-37888-X.
  14. ↑ Lorenz (2008) p.116
  15. ↑ Lorenz (2008) p.119
  16. 1 2 3 Serre (1997) p.88
  17. 1 2 Fried & Jarden (2008) p.459
  18. ↑ Terjanian, Guy (1966). "Un contre-example à une conjecture d'Artin". C. R. Acad. Sci. Paris Sér. A-B (in French) 262: A612. Zbl 0133.29705.
  19. ↑ Lang (1997) p.247
  20. ↑ Fried & Jarden (2008) p.457
  21. 1 2 3 4 Fried & Jarden (2008) p.461

References

This article is issued from Wikipedia - version of the Thursday, January 21, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.