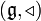Quasi-Frobenius Lie algebra
In mathematics, a quasi-Frobenius Lie algebra
over a field  is a Lie algebra
is a Lie algebra
equipped with a nondegenerate skew-symmetric bilinear form
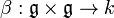 , which is a Lie algebra 2-cocycle of
, which is a Lie algebra 2-cocycle of 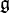 with values in
with values in  . In other words,
. In other words,
for all  ,
, 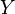 ,
, 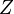 in
in 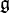 .
.
If 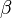 is a coboundary, which means that there exists a linear form
is a coboundary, which means that there exists a linear form  such that
such that
then
is called a Frobenius Lie algebra.
Equivalence with pre-Lie algebras with nondegenerate invariant skew-symmetric bilinear form
If ![(\mathfrak{g},[\,\,\,,\,\,\,],\beta )](../I/m/e6778bc97f09d2f373e33027c0e6642b.png) is a quasi-Frobenius Lie algebra, one can define on
is a quasi-Frobenius Lie algebra, one can define on 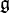 another bilinear product
another bilinear product 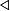 by the formula
by the formula
![\beta \left(\left[X,Y\right],Z\right)=\beta \left(Z \triangleleft Y,X \right)](../I/m/69f812329abf26f4a3c10418552b7c7c.png) .
.
Then one has
![\left[X,Y\right]=X \triangleleft Y-Y \triangleleft X](../I/m/c11e9fb7cec91db3a22d827613696851.png) and
and
is a pre-Lie algebra.
See also
References
- Jacobson, Nathan, Lie algebras, Republication of the 1962 original. Dover Publications, Inc., New York, 1979. ISBN 0-486-63832-4
- Vyjayanthi Chari and Andrew Pressley, A Guide to Quantum Groups, (1994), Cambridge University Press, Cambridge ISBN 0-521-55884-0.
This article is issued from Wikipedia - version of the Tuesday, November 17, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
![(\mathfrak{g},[\,\,\,,\,\,\,] )](../I/m/7a202d338024a90e91c3f5b17bfb4cf0.png)
![\beta \left(\left[X,Y\right],Z\right)+\beta \left(\left[Z,X\right],Y\right)+\beta \left(\left[Y,Z\right],X\right)=0](../I/m/08571fc40803fb0b50e8e1d28f2fab8d.png)
![\beta(X,Y)=f(\left[X,Y\right]),](../I/m/853223266d9610ce6c1042a3f28d6ed7.png)