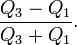Quartile coefficient of dispersion
In statistics, the quartile coefficient of dispersion is a descriptive statistic which measures dispersion and which is used to make comparisons within and between data sets.
The statistic is easily computed using the first (Q1) and third (Q3) quartiles for each data set. The quartile coefficient of dispersion is:[1]
Example
Consider the following two data sets:
- A = {2, 4, 6, 8, 10, 12, 14}
- n = 7, range = 12, mean = 8, median = 8, Q1 = 4, Q3 = 12, coefficient of dispersion = 0.5
- B = {1.8, 2, 2.1, 2.4, 2.6, 2.9, 3}
- n = 7, range = 1.2, mean = 2.4, median = 2.4, Q1 = 2, Q3 = 2.9, coefficient of dispersion = 0.18
The quartile coefficient of dispersion of data set A is 2.7 times as great (0.5 / 0.18) as that of data set B.
See also
References
- ↑ Bonett, D. G. (2006). "Confidence interval for a coefficient of quartile variation". Computational Statistics & Data Analysis 50 (11): 2953–2957. doi:10.1016/j.csda.2005.05.007.
This article is issued from Wikipedia - version of the Friday, September 04, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.