Quantum ergodicity
In quantum chaos, a branch of mathematical physics, quantum ergodicity is a property of the quantization of classical mechanical systems that are chaotic in the sense of exponential sensitivity to initial conditions. Quantum ergodicity states, roughly, that in the high-energy limit, the probability distributions associated to energy eigenstates of a quantized ergodic Hamiltonian tend to a uniform distribution in the classical phase space. This is consistent with the intuition that the flows of ergodic systems are equidistributed in phase space. By contrast, classical completely integrable systems generally have periodic orbits in phase space, and this is exhibited in a variety of ways in the high-energy limit of the eigenstates: typically that some form of concentration or "scarring" occurs in the limit.
The model case of a Hamiltonian is the geodesic Hamiltonian on the cotangent bundle of a compact Riemannian manifold. The quantization of the geodesic flow is given by the fundamental solution of the Schrödinger equation
where 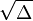 is the square root of the Laplace-Beltrami operator. The quantum ergodicity theorem of Shnirelman, Yves Colin de Verdière, and Zelditch states that a compact Riemannian manifold whose unit tangent bundle is ergodic under the geodesic flow is also ergodic in the sense that the probability density associated to the nth eigenfunction of the Laplacian tends weakly to the uniform distribution on the unit cotangent bundle as n → ∞. Quantum ergodicity can be formulated as a non-commutative analogue of the classical ergodicity (T. Sunada).
is the square root of the Laplace-Beltrami operator. The quantum ergodicity theorem of Shnirelman, Yves Colin de Verdière, and Zelditch states that a compact Riemannian manifold whose unit tangent bundle is ergodic under the geodesic flow is also ergodic in the sense that the probability density associated to the nth eigenfunction of the Laplacian tends weakly to the uniform distribution on the unit cotangent bundle as n → ∞. Quantum ergodicity can be formulated as a non-commutative analogue of the classical ergodicity (T. Sunada).
See also
References
- Zelditch, S (2006), "Quantum ergodicity and mixing of eigenfunctions", in Françoise, Jean-Pierre; Naber, Gregory L.; Tsun, Tsou Sheung, Encyclopedia of mathematical physics. Vol. 1, 2, 3, 4, 5, Academic Press/Elsevier Science, Oxford, ISBN 9780125126601, MR 2238867
- Sunada, T (1997), "Quantum ergodicity", Trend in Mathematics, Birkhauser Verlag, Basel, pp. 175–196