Quantum spin liquid
In condensed matter physics, quantum spin liquid is a state that can be achieved in a system of interacting quantum spins. The state is referred to as a "liquid" as it is a disordered state in comparison to a ferromagnetic spin state,[1] much in the way liquid water is in a disordered state compared to crystalline ice. However, unlike other disordered states, a quantum spin liquid state preserves its disorder to very low temperatures.[2]
The quantum spin liquid state was first proposed by physicist Phil Anderson in 1973 as the ground state for a system of spins on a triangular lattice that interact with their nearest neighbors via the so-called antiferromagnetic interaction. Quantum spin liquids generated further interest when in 1987 Anderson proposed a theory that described high temperature superconductivity in terms of a disordered spin-liquid state.[3] A quantum spin liquid state in κ-(BEDT-TTF)2Cu2(CN)3 was first thoroughly mapped using muon spin spectroscopy by a team led by Dr Francis Pratt at ISIS neutron source, UK in March, 2011.[4]
Examples
Several physical models have a disordered ground state that can be described as a quantum spin liquid.
Frustrated magnetic moments

Localized spins are frustrated if there exist competing exchange interactions that can not all be satisfied at the same time, leading to a large degeneracy of the system's ground state. A triangle of Ising spins (meaning the only possible orientations of the spins are "up" and "down"), which interact antiferromagnetically, is a simple example for frustration. In the ground state, two of the spins can be antiparallel but the third one cannot. This leads to an increase of possible orientations (six in this case) of the spins in the ground state, enhancing fluctuations and thus suppressing magnetic ordering.
Some frustrated materials with different lattice structures and their Curie-Weiss temperature are listed in the table.[2] All of them are proposed spin liquid candidates.
| Material | Lattice | ![\Theta _{cw} [K]](../I/m/b83027a986787b24b8b471040d36b087.png) |
|---|---|---|
| κ-(BEDT-TTF)2Cu2(CN)3 | anisotropic triangular | -375 |
| ZnCu3(OH)6Cl2 (herbertsmithite) | Kagome | -241 |
| BaCu3V2O8(OH)2 (vesignieite) | Kagome | |
| Na4Ir3O8 | Hyperkagome | -650 |
| Cu-(1,3-benzenedicarboxylate) | Kagome | -33 [5] |
| Rb2Cu3SnF12 | Kagome | [6] |
Resonating valence bonds (RVB)

To build a ground state without magnetic moment, valence bond states can be used, where two electron spins form a spin 0 singlet due to the antiferromagnetic interaction. If every spin in the system is bound like this, the state of the system as a whole has spin 0 too and is non-magnetic. The two spins forming the bond are maximally entangled, while not being entangled with the other spins. If all spins are distributed to certain localized static bonds, this is called a valence bond solid (VBS).
There are two things that still distinguish a VBS from a spin liquid: First, by ordering the bonds in a certain way, the lattice symmetry is usually broken, which is not the case for a spin liquid. Second, this ground state lacks long-range entanglement. To achieve this, quantum mechanical fluctuations of the valence bonds must be allowed, leading to a ground state consisting of a superposition of many different partitionings of spins into valence bonds. If the partitionings are equally distributed (with the same quantum amplitude), there is no preference for any specific partitioning ("valence bond liquid"). This kind of ground state wavefunction was proposed by P. W. Anderson in 1973 as the ground state of spin liquids[7] and is called a resonating valence bond (RVB) state. These states are of great theoretical interest as they are proposed to play a key role in high-temperature superconductor physics.[8]
-

One possible short-range pairing of spins in a RVB state.
-

Long-range pairing of spins.
Excitations

The valence bonds do not have to be formed by nearest neighbors only and their distributions
may vary in different materials. Ground states with large contributions of long range
valence bonds have more low-energy spin excitations, as those valence bonds are easier to
break up. On breaking, they form two free spins. Other excitations rearrange the valence bonds, leading to low-energy excitations even for short-range bonds.
Very special about spin liquids is, that they support exotic excitations, meaning
excitations with fractional quantum numbers. A prominent example is the excitation of
spinons which are neutral in charge and carry spin 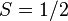 .
In spin liquids, a spinon is created if one spin is not paired in a valence bond. It can move by rearranging nearby valence bonds at low energy cost.
.
In spin liquids, a spinon is created if one spin is not paired in a valence bond. It can move by rearranging nearby valence bonds at low energy cost.
Realizations of (stable) RVB states
The first discussion of the RVB state on square lattice using the RVB picture[9] only consider nearest neighbour bonds that connect different sub-lattices.
The constructed RVB state is an equal amplitude superposition of all the nearest-neighbour bond configurations. Such a RVB state is believed to contain emergent gapless  gauge field which may confine the spinons etc. So the equal-amplitude nearest-neighbour RVB state on square lattice is unstable and may describe a critical phase transition point between two stable phases. A version of RVB state which is stable and contains deconfined spinons is the chiral spin state.[10][11] Later, another version of stable RVB state with deconfined spinons, the Z2 spin liquid, is proposed,[12][13] which realizes the simplest topological order -- Z2 topological order. Both chiral spin state and Z2 spin liquid state have RVB bonds that connect the same sub-lattice.
In chiral spin state, different bond configurations can have complex amplitudes, while
in Z2 spin liquid state, different bond configurations only have real amplitudes.
The RVB state on triangle lattice also realizes the Z2 spin liquid,[14] where
different bond configurations only have real amplitudes. The toric code model is yet another realization of
Z2 spin liquid (and Z2 topological order) that explicitly breaks the spin rotation symmetry and is exactly soluble.[15]
gauge field which may confine the spinons etc. So the equal-amplitude nearest-neighbour RVB state on square lattice is unstable and may describe a critical phase transition point between two stable phases. A version of RVB state which is stable and contains deconfined spinons is the chiral spin state.[10][11] Later, another version of stable RVB state with deconfined spinons, the Z2 spin liquid, is proposed,[12][13] which realizes the simplest topological order -- Z2 topological order. Both chiral spin state and Z2 spin liquid state have RVB bonds that connect the same sub-lattice.
In chiral spin state, different bond configurations can have complex amplitudes, while
in Z2 spin liquid state, different bond configurations only have real amplitudes.
The RVB state on triangle lattice also realizes the Z2 spin liquid,[14] where
different bond configurations only have real amplitudes. The toric code model is yet another realization of
Z2 spin liquid (and Z2 topological order) that explicitly breaks the spin rotation symmetry and is exactly soluble.[15]
Identification in Experiments
Since there is no single experimental feature which identifies a material as a spin liquid, several experiments have to be conducted to gain information on different properties which characterize a spin liquid. An indication is given by a large value of the frustration parameter 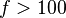 , which is defined as
, which is defined as
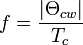
where 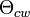 is the Curie-Weiss temperature and
is the Curie-Weiss temperature and 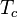 is the temperature below which magnetic order begins to develop.
is the temperature below which magnetic order begins to develop.
One of the most direct evidence for absence of magnetic ordering give NMR or µSR experiments. If there is a local magnetic field present, the nuclear or muon spin would be affected which can be measured. 1H-NMR measurements [16] on κ-(BEDT-TTF)2Cu2(CN)3 have shown no sign of magnetic ordering down to 32 mK, which is four orders of magnitude smaller than the coupling constant J≈250 K[17] between neighboring spins in this compound. Further investigations include:
- Specific heat measurements give information about the low-energy density of states, which can be compared to theoretical models.
- Thermal transport measurements can determine if excitations are localized or itinerant.
- Neutron scattering gives information about the nature of excitations and correlations (e.g. spinons).
- Reflectance measurements can uncover spinons, which couple via emergent gauge fields to the electromagnetic field, giving rise to a power-law optical conductivity.[18]

Observation of fractionalization
In 2012, Young Lee and his collaborators at MIT and the National Institute of Standards and Technology artificially developed a crystal of herbertsmithite, a crystal with kagome lattice ordering, on which they were able to perform neutron scattering experiments.[19] The experiments revealed evidence for spin-state fractionalization, a predicted property of quantum spin-liquid type states.[20] The observation has been described as a hallmark for the quantum spin liquid state in herbertsmithite.[21] Data indicate that the strongly correlated quantum spin liquid, a specific form of quantum spin liquid, is realized in Herbertsmithite.[22]
Applications
Materials supporting quantum spin liquid states may have applications in data storage and memory.[23] In particular, it is possible to realize topological quantum computation by means of spin-liquid states.[24] Developments in quantum spin liquids may also help in the understanding of high temperature superconductivity.[25]
References
- ↑ Wilkins, Alasdair (August 15, 2011). "A Strange New Quantum State of Matter: Spin Liquids". io9. Retrieved 23 December 2012.
- 1 2 Leon Balents (2010). "Spin liquids in frustrated magnets". Nature 464 (7286): 199–208. Bibcode:2010Natur.464..199B. doi:10.1038/nature08917. PMID 20220838.
- ↑ Trafton, Anne (March 28, 2011). "A new spin on superconductivity?". MIT News. Retrieved 24 December 2012.
- ↑ "Quantum mapmakers complete first voyage through spin liquid". ISIS neutron and muon source. Retrieved 23 August 2013.
- ↑ Emily A. Nytko, Joel S. Helton, Peter Müller, and Daniel G. Nocera A Structurally Perfect S = 1/2 Metal−Organic Hybrid Kagome Antiferromagnet J. Am. Chem. Soc. 2008; 130(10), pp 2922–2923 doi:10.1021/ja709991u
- ↑ Matan, K.; Ono, T.; Fukumoto, Y.; Sato, T. J.; et al. (2010). "Pinwheel valence-bond solid and triplet excitations in the two-dimensional deformed kagome lattice". Nature Physics 6: 865–869. arXiv:1007.3625. Bibcode:2010NatPh...6..865M. doi:10.1038/nphys1761.
- ↑ P. W. Anderson (1973). "Resonating valence bonds: A new kind of insulator?". Mater. Res. Bull. 8 (2). doi:10.1016/0025-5408(73)90167-0.
- ↑ P. W. Anderson (1987). "The resonating valence bond state in La2CuO4 and superconductivity". Science 235 (4793): 1196–1198. Bibcode:1987Sci...235.1196A. doi:10.1126/science.235.4793.1196. PMID 17818979.
- ↑ Kivelson, Steven A.; Rokhsar, Daniel S.; Sethna, James P. (1987). "Topology of the resonating valence-bond state: Solitons and high-Tc superconductivity". Phys. Rev. B 35: 8865. Bibcode:1987PhRvB..35.8865K. doi:10.1103/physrevb.35.8865.
- ↑ Kalmeyer, V.; Laughlin, R. B. (1987). "Equivalence of the resonating-valence-bond and fractional quantum Hall states". , Phys. Rev. Lett. 59: 2095. Bibcode:1987PhRvL..59.2095K. doi:10.1103/physrevlett.59.2095.
- ↑ Wen, Xiao-Gang; Wilczek, F.; Zee, A. (1989). "Chiral Spin States and Superconductivity". , Phys. Rev. B 39: 11413. Bibcode:1989PhRvB..3911413W. doi:10.1103/physrevb.39.11413.
- ↑ Read, N.; Sachdev, Subir (1991). "Large-N expansion for frustrated quantum antiferromagnets". , Phys. Rev. Lett. 66: 1773. Bibcode:1991PhRvL..66.1773R. doi:10.1103/physrevlett.66.1773.
- ↑ Wen, Xiao-Gang (1991). "Mean Field Theory of Spin Liquid States with Finite Energy Gaps". , Phys. Rev. B 44: 2664. Bibcode:1991PhRvB..44.2664W. doi:10.1103/physrevb.44.2664.
- ↑ R. Moessner, S. L. Sondhi, Phys. Rev. Lett 86, 1881 (2001); arXiv:cond-mat/0205029
- ↑ A. Yu. Kitaev, Annals Phys., 303, 2 (2003); arXiv:quant-ph/9707021
- ↑ Y. Shimizu; K. Miyagawa; K. Kanoda; M. Maesato; et al. (2003). "Spin Liquid State in an Organic Mott Insulator with a Triangular Lattice". Phys. Rev. Lett. 91 (10). arXiv:cond-mat/0307483. Bibcode:2003PhRvL..91j7001S. doi:10.1103/PhysRevLett.91.107001.
- ↑ In literature, the value of J is commonly given in units of temperature (
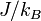 ) instead of energy.
) instead of energy. - ↑ T. Ng & P. A. Lee (2007). "Power-Law Conductivity inside the Mott Gap: Application to κ-(BEDT-TTF)2Cu2(CN)3". Phys. Rev. Lett. 99 (15). arXiv:0706.0050. Bibcode:2007PhRvL..99o6402N. doi:10.1103/PhysRevLett.99.156402.
- ↑ Anthony, Sebastian. "MIT discovers a new state of matter, a new kind of magnetism". Extremetech. Retrieved 23 August 2013.
- ↑ "Third State Of Magnetism Discovered By MIT Researchers". Red Orbit. December 21, 2012. Retrieved 24 December 2012.
- ↑ Han, Tiang-Heng; Young S. Lee; et al. (2012). "Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet". Nature 492 (7429). arXiv:1307.5047. Bibcode:2012Natur.492..406H. doi:10.1038/nature11659. Retrieved 24 December 2012.
- ↑ Amusia, M., Popov, K., Shaginyan, V., Stephanovich, V. (2014). "Theory of Heavy-Fermion Compounds - Theory of Strongly Correlated Fermi-Systems". Springer. ISBN 978-3-319-10825-4.
- ↑ Aguilar, Mario (December 20, 2012). "This Weird Crystal Demonstrates a New Magnetic Behavior That Works Like Magic". Gizmodo. Retrieved 24 December 2012.
- ↑ Fendley, Paul. "Topological Quantum Computation from non-abelian anyons" (PDF). University of Virginia. Retrieved 24 December 2012.
- ↑ Chandler, David (December 20, 2012). "New kind of magnetism discovered: Experiments demonstrate 'quantum spin liquid'". Phys.org. Retrieved 24 December 2012.