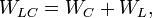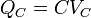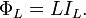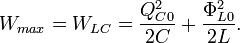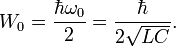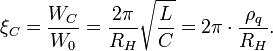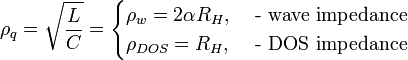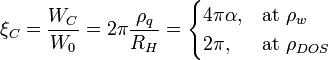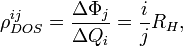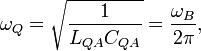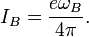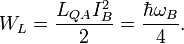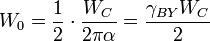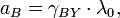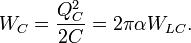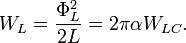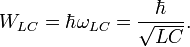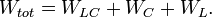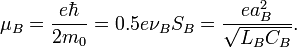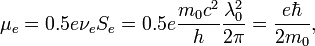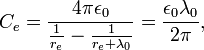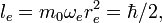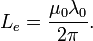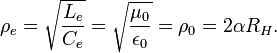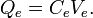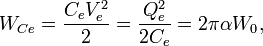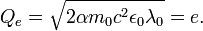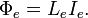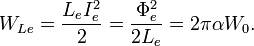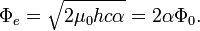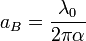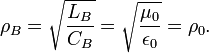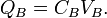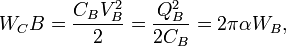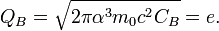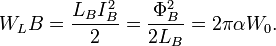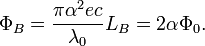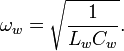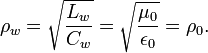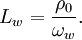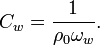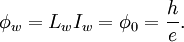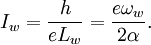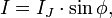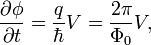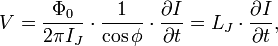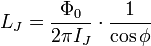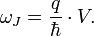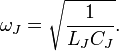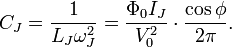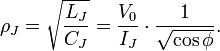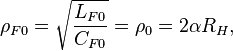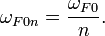Quantum LC circuit
An LC circuit can be quantized using the same methods as for the quantum harmonic oscillator. An LC circuit is a variety of resonant circuit, and consists of an inductor, represented by the letter L, and a capacitor, represented by the letter C. When connected together, an electric current can alternate between them at the circuit's resonant frequency:
where L is the inductance in henries, and C is the capacitance in farads. The angular frequency 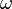 has units of radians per second. A capacitor stores energy in the electric field between the plates, which can be written as follows:
has units of radians per second. A capacitor stores energy in the electric field between the plates, which can be written as follows:
Where Q is the net charge on the capacitor, calculated as
Likewise, an inductor stores energy in the magnetic field depending on the current, which can be written as follows:
Where  is the branch flux, defined as
is the branch flux, defined as
Since charge and flux are canonically conjugate variables, one can use canonical quantization to rewrite the classical hamiltonian in the quantum formalism, by identifying
and enforcing the canonical commutation relation
One-dimensional harmonic oscillator
Hamiltonian and energy eigenstates


Like the one-dimensional harmonic oscillator problem, an LC circuit can be quantized by either solving the Schrödinger equation or using creation and annihilation operators. The energy stored in the inductor can be looked at as a "kinetic energy term" and the energy stored in the capacitor can be looked at as a "potential energy term".
The Hamiltonian of such a system is:
where Q is the charge operator, and  is the magnetic flux operator. The first term represents the energy stored in an inductor, and the second term represents the energy stored in a capacitor. In order to find the energy levels and the corresponding energy eigenstates, we must solve the time-independent Schrödinger equation,
is the magnetic flux operator. The first term represents the energy stored in an inductor, and the second term represents the energy stored in a capacitor. In order to find the energy levels and the corresponding energy eigenstates, we must solve the time-independent Schrödinger equation,
Since an LC circuit really is an electrical analog to the harmonic oscillator, solving the Schrödinger equation yields a family of solutions (the Hermite polynomials).
Magnetic Flux as a Conjugate Variable
A completely equivalent solution can be found using magnetic flux as the conjugate variable where the conjugate "momentum" is equal to capacitance times the time derivative of magnetic flux. The conjugate "momentum" is really the charge.
Using Kirchhoff's Junction Rule, the following relationship can be obtained:
Since 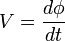 , the above equation can be written as follows:
, the above equation can be written as follows:
Converting this into a Hamiltonian, one can develop a Schrödinger equation as follows:
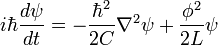 where
where 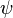 is a function of magnetic flux
is a function of magnetic flux
Quantization of coupled LC circuits
Two inductively coupled LC circuits have a non-zero mutual inductance. This is equivalent to a pair of harmonic oscillators with a kinetic coupling term.
The Lagrangian for an inductively coupled pair of LC circuits is as follows:
As usual, the Hamiltonian is obtained by a Legendre transform of the Lagrangian.
Promoting the observables to quantum mechanical operators yields the following Schrödinger equation.
One cannot proceed further using the above coordinates because of the coupled term. However, a coordinate transformation from the wave function as a function of both charges to the wave function as a function of the charge difference 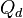 , where
, where 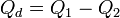 and a coordinate
and a coordinate 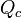 (somewhat analogous to a "Center-of-Mass"), the above Hamiltonian can be solved using the Separation of Variables technique.
(somewhat analogous to a "Center-of-Mass"), the above Hamiltonian can be solved using the Separation of Variables technique.
The CM coordinate is as seen below:
The Hamiltonian under the new coordinate system is as follows:
In the above equation  is equal to
is equal to 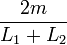 and
and  equals the reduced inductance.
equals the reduced inductance.
The separation of variables technique yields two equations, one for the "CM" coordinate that is the differential equation of a free particle, and the other for the charge difference coordinate, which is the Schrödinger equation for a harmonic oscillator.
The solution for the first differential equation once the time dependence is appended resembles a plane wave, while the solution of the second differential equation is seen above.
Hamiltonian mechanics
Classical case
Stored energy (Hamiltonian) for classical LC circuit:
Hamiltonian's equations:
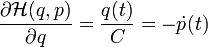
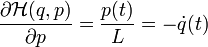 ,
,
where 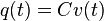 stored capacitor charge (or electric flux) and
stored capacitor charge (or electric flux) and  magnetic momentum (magnetic flux),
magnetic momentum (magnetic flux),
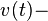 capacitor voltage and
capacitor voltage and 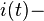 inductance current,
inductance current, 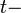 time variable.
time variable.
Nonzero initial conditions:
At 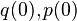 we shall have oscillation frequency:
we shall have oscillation frequency:
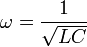 ,
,
and wave impedance of the LC circuit (without dissipation):
Hamiltonian's equations solutions:
At 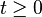 we shall have the following values of charges, magnetic flux and energy:
we shall have the following values of charges, magnetic flux and energy:
Definition of the Phasor
In the general case the wave amplitudes can be defined in the complex space
where  .
.
 ,
,
where 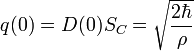 - electric charge at zero time,
- electric charge at zero time, 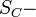 capacitance area.
capacitance area.
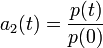 ,
,
where 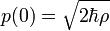 - magnetic flux at zero time,
- magnetic flux at zero time,
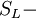 inductance area.
Note that, at the equal area elements
inductance area.
Note that, at the equal area elements
we shall have the following relationship for the wave impedance:
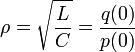 .
.
Wave amplitude and energy could be defined as:
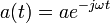
![\mathcal{H} = \hbar \omega [a_1^2(t) + a_2^2(t)] = \hbar \omega |a|^2 \](../I/m/4056008ea9350e021151db54616a03a5.png) .
.
Quantum case
In the quantum case we have the following definition for momentum operator:
Momentum and charge operators produce the following commutator:
![[\hat{q},\hat{p}] = j\hbar \](../I/m/24b1c8dd6d002d194ab49eb6b564d423.png) .
.
Amplitude operator can be defined as:
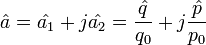 ,
,
and phazor:
 .
.
Hamilton's operator will be:
Amplitudes commutators:
![[\hat{a}_1(t),\hat{a}_2(t)] = j/2 \](../I/m/1d3ddb25f6641d47631d685b4dc0d627.png)
![[\hat{a}(t),\hat{a}^\dagger(t)] = 1 \](../I/m/813e287da4549527f5ef6d09232e6af7.png) .
.
Heisenberg uncertainty principle:
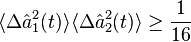 .
.
Wave impedance of free space
When wave impedance of quantum LC circuit takes the value of free space
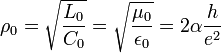 ,
,
where 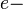 electron charge and
electron charge and 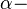 fine structure constant,
then "electric" and "magnetic" fluxes at zero time point will be:
fine structure constant,
then "electric" and "magnetic" fluxes at zero time point will be:
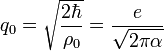
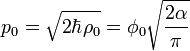 ,
,
where 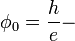 magnetic flux quantum.
magnetic flux quantum.
Quantum LC circuit paradox
General formulation
In the classical case the energy of LC circuit will be:
where 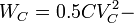 capacitance energy, and
capacitance energy, and
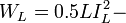 inductance energy. Furthermore, there are the following relationships between charges (electric or magnetic) and voltages or currents:
inductance energy. Furthermore, there are the following relationships between charges (electric or magnetic) and voltages or currents:
Therefore, the maximal values of capacitance and inductance energies will be:
Note that the resonance frequency 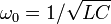 has nothing to do with the energy in the classical case. But it has the following relationship with energy in the quantum case:
has nothing to do with the energy in the classical case. But it has the following relationship with energy in the quantum case:
So, in the quantum case, by filling capacitance with the one electron charge:
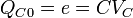 and
and 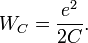
The relationship between capacitance energy and the ground state oscillator energy will then be:
where 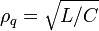 quantum impedance of LC circuit.
The quantum impedance of the quantum LC circuit could be in practice of the two types:
quantum impedance of LC circuit.
The quantum impedance of the quantum LC circuit could be in practice of the two types:
So, the energy relationships will be:
and that is the main problem of the quantum LC circuit: energies stored on capacitance and inductance are not equal to the ground state energy of the quantum oscillator. This energy problem produces the quantum LC circuit paradox (QLCCP).
Possible solution
Some simple solution of the QLCCP could be found in the following way. Yakymakha (1989) [1](eqn.30) proposed the following DOS quantum impedance definition:
where 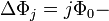 magnetic flux, and
magnetic flux, and
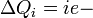 electric flux,
electric flux, 
So, there are no electric or magnetic charges in the quantum LC circuit, but electric and magnetic fluxes only. Therefore, not only in the DOS LC circuit, but in the other LC circuits too, there are only the electromagnetic waves. Thus, the quantum LC circuit is the minimal geometrical-topological value of the quantum waveguide, in which there are no electric or magnetic charges, but electromagnetic waves only. Now one should consider the quantum LC circuit as a "black wave box" (BWB), which has no electric or magnetic charges, but waves. Furthermore, this BWB could be "closed" (in Bohr atom or in the vacuum for photons), or "open" (as for QHE and Josephson junction). So, the quantum LC circuit should has BWB and "input - output" supplements. The total energy balance should be calculated with considering of "input" and "output" devices. Without "input - output" devices, the energies "stored" on capacitances and inductances are virtual or "characteristics", as in the case of characteristic impedance (without dissipation). Very close to this approach now are Devoret (2004),[2] which consider Josephson junctions with quantum inductance, Datta impedance of Schrödinger waves (2008) and Tsu (2008),[3] which consider quantum wave guides.
Explanation for DOS quantum LC circuit
As presented below, the resonance frequency for QHE is:
where  cyclotron frequency,
cyclotron frequency,
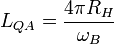 and
and
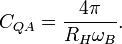 The scaling current for QHE will be:
The scaling current for QHE will be:
Therefore, the inductance energy will be:
So for quantum magnetic flux 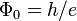 , inductance energy is half as much as the ground state oscillation energy. This is due to the spin of electron (there are two electrons on Landau level on the same quantum area element). Therefore, the inductance/capacitance energy considers the total Landau level energy per spin.
, inductance energy is half as much as the ground state oscillation energy. This is due to the spin of electron (there are two electrons on Landau level on the same quantum area element). Therefore, the inductance/capacitance energy considers the total Landau level energy per spin.
Explanation for "wave" quantum LC circuit
By analogy to the DOS LC circuit, we have
two times lesser value due to the spin. But here there is the new dimensionless fundamental constant:
which considers topological properties of the quantum LC circuit. This fundamental constant first appeared in the Bohr atom for Bohr radius:
where 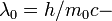 Compton wavelength of electron.
Compton wavelength of electron.
Thus, the wave quantum LC circuit has no charges in it, but electromagnetic waves only. So capacitance or inductance "characteristic energies" are
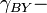 times less than the total energy of the oscillator. In other words, charges "disappear" at the "input" and "generate" at the "output" of the wave LC circuit, adding energies to keep balance.
times less than the total energy of the oscillator. In other words, charges "disappear" at the "input" and "generate" at the "output" of the wave LC circuit, adding energies to keep balance.
Total energy of quantum LC circuit
Energy stored on the quantum capacitance:
Energy stored on the quantum inductance:
Resonance energy of the quantum LC circuit:
Thus, the total energy of the quantum LC circuit should be:
In the general case, resonance energy 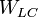 could be due to the "rest mass" of electron, energy gap for Bohr atom, etc.
However, energy stored on capacitance
could be due to the "rest mass" of electron, energy gap for Bohr atom, etc.
However, energy stored on capacitance  is due to electric charge. Actually, for free electron and Bohr atom LC circuits we have quantized electric fluxes, equal to the electronic charge,
is due to electric charge. Actually, for free electron and Bohr atom LC circuits we have quantized electric fluxes, equal to the electronic charge,
 .
.
Furthermore, energy stored on inductance 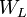 is due to magnetic momentum. Actually, for Bohr atom we have Bohr Magneton:
is due to magnetic momentum. Actually, for Bohr atom we have Bohr Magneton:
In the case of free electron, Bohr Magneton will be:
the same, as for Bohr atom.
Applications
Electron as LC circuit
Electron capacitance could be presented as the spherical capacitor:
where  electron radius and
electron radius and  Compton wavelength.
Compton wavelength.
Note, that this electron radius is consistent with the standard definition of the spin. Actually, rotating momentum of electron is:
where 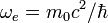 is considered.
is considered.
Spherical inductance of electron:
Characterictic impedance of electron:
Resonance frequency of electron LC circuit:
Induced electric flux on electron capacitance:
Energy, stored on electron capacitance:
where 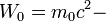 is the "rest energy" of electron. So, induced electric flux will be:
is the "rest energy" of electron. So, induced electric flux will be:
Thus, through electron capacitance we have quantized electric flux, equal to the electron charge.
Magnetic flux through inductance:
Magnetic energy, stored on inductance:
So, induced magnetic flux will be:
where 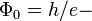 magnetic flux quantum. Thus, through electron inductance there are no quantization of magnetic flux.
magnetic flux quantum. Thus, through electron inductance there are no quantization of magnetic flux.
Bohr atom as LC circuit
Bohr radius:
where 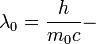 Compton wavelength of electron,
Compton wavelength of electron,
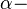 fine structure constant.
fine structure constant.
Bohr atomic surface:
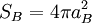 .
.
Bohr inductance:
 .
.
Bohr capacitance:
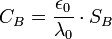 .
.
Bohr wave impedance:
Bohr angular frequency:
where 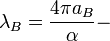 Bohr wavelength for the first energy level.
Bohr wavelength for the first energy level.
Induced electric flux of the Bohr first energy level:
Energy, stored on the Bohr capacitance:
where  is the Bohr energy. So, induced electric flux will be:
is the Bohr energy. So, induced electric flux will be:
Thus, through the Bohr capacitance we have quantized electric flux, equal to the electron charge.
Magnetic flux through the Bohr inductance:
So, induced magnetic flux will be:
Thus, through the Bohr inductance there are no quantization of magnetic flux.
Photon as LC circuit
Photon "resonant angular frequency":
Photon "wave impedance":
Photon "wave inductance":
Photon "wave capacitance":
Photon "magnetic flux quantum":
Photon "wave current":
Quantum Hall effect as LC circuit
In the general case 2D- density of states (DOS) in a solid could be defined by the following:
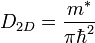 ,
,
where 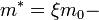 current carriers effective mass in a solid,
current carriers effective mass in a solid, 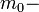 electron mass, and
electron mass, and 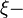 dimensionless parameter, which considers band structure of a solid. So, the quantum inductance can be defined as follows:
dimensionless parameter, which considers band structure of a solid. So, the quantum inductance can be defined as follows:
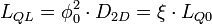 ,
,
where 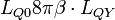 - the ‘’ideal value’’ of quantum inductance at
- the ‘’ideal value’’ of quantum inductance at 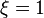 and another ideal quantum inductance:
and another ideal quantum inductance:
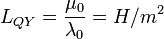 , (3)
, (3)
where 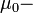 magnetic constant,
magnetic constant,
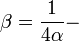 magnetic "fine structure constant"[4](p. 62),
magnetic "fine structure constant"[4](p. 62), 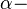 fine structure constant and
fine structure constant and  Compton wavelength of electron, first defined by Yakymakha (1994)[5] in the spectroscopic investigations of the silicon MOSFETs.
Compton wavelength of electron, first defined by Yakymakha (1994)[5] in the spectroscopic investigations of the silicon MOSFETs.
Since defined above quantum inductance is per unit area, therefore its absolute value will be in the QHE mode:
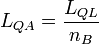 ,
,
where the carrier concentration is:
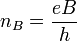 ,
,
and  is the Planck constant.
By analogically, the absolute value of the quantum capacitance will be in the QHE mode:
is the Planck constant.
By analogically, the absolute value of the quantum capacitance will be in the QHE mode:
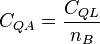 ,
,
where
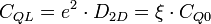 ,
,
is DOS definition of the quantum capacitance according to Luryi,[6] 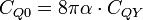 - quantum capacitance ‘’ideal value’’ at
- quantum capacitance ‘’ideal value’’ at 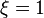 , and other quantum capacitance:
, and other quantum capacitance:
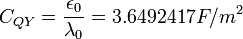 ,
,
where 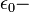 dielectric constant, first defined by Yakymakha (1994)[5] > in the spectroscopic investigations of the silicon MOSFETs.
The standard wave impedance definition for the QHE LC circuit could be presented as:
dielectric constant, first defined by Yakymakha (1994)[5] > in the spectroscopic investigations of the silicon MOSFETs.
The standard wave impedance definition for the QHE LC circuit could be presented as:
 ,
,
where 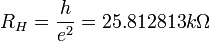 von Klitzing constant for resistance.
von Klitzing constant for resistance.
The standard resonant frequency definition for the QHE LC circuit could be presented as:
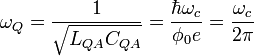 ,
,
where 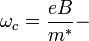 standard cyclotron frequency in the magnetic field B.
standard cyclotron frequency in the magnetic field B.
Hall scaling current quantum will be
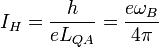 ,
,
where  Hall angular frequency.
Hall angular frequency.
Josephson junction as LC circuit
Electromagnetic induction (Faraday) low:
where 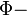 magnetic flux,
magnetic flux, 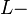 Josephson junction quantum inductance and
Josephson junction quantum inductance and
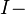 Josephson junction current.
DC Josephson equation for current:
Josephson junction current.
DC Josephson equation for current:
where 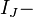 Josephson scale for current,
Josephson scale for current,
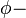 phase difference between superconductors.
Current derivative on time variable will be:
phase difference between superconductors.
Current derivative on time variable will be:
AC Josephson equation:
where 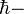 reduced Planck constant,
reduced Planck constant, 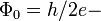 Josephson magnetic flux quantum,
Josephson magnetic flux quantum,
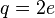 and
and 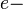 electron charge.
Combining equations for derivatives yields junction voltage:
electron charge.
Combining equations for derivatives yields junction voltage:
where
is the Devoret (1997) [7] quantum inductance.
AC Josephson equation for angular frequency:
Resonance frequency for Josephson LC circuit:
where 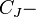 is the Devoret quantum capacitance, that can be defined as:
is the Devoret quantum capacitance, that can be defined as:
Quantum wave impedance of Josephson junction:
For 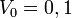 mV and
mV and 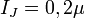 A wave impedance will be
A wave impedance will be 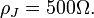
Flat Atom as LC circuit
Quantum capacitance of Flat Atom (FA):
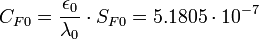 F,
F,
where 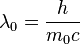 .
.
Quantum inductance of FA:
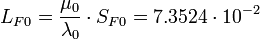 H.
H.
Quantum area element of FA:
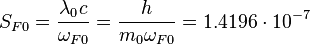 m2.
m2.
Resonance frequency of FA:
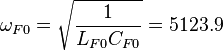 rad/s.
rad/s.
Characteristic impedunce of FA:
where 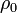 is the impedance of free space.
is the impedance of free space.
Total electric charge on the first energy level of FA:
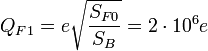 ,
,
where 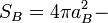 Bohr quantum area element.
First FA was discovered by Yakymakha (1994) [5] as very low frequency resonance on the p- channel MOSFETs.
Contrary to the spherical Bohr atom, the FA has gyperbolic dependence on the number of energy level (n) [8]
Bohr quantum area element.
First FA was discovered by Yakymakha (1994) [5] as very low frequency resonance on the p- channel MOSFETs.
Contrary to the spherical Bohr atom, the FA has gyperbolic dependence on the number of energy level (n) [8]
See also
References
- ↑ Yakymakha O.L.(1989). High Temperature Quantum Galvanomagnetic Effects in the Two- Dimensional Inversion Layers of MOSFET's (In Russian). Kyiv: Vyscha Shkola. p. 91. ISBN 5-11-002309-3. djvu</
- ↑ Devoret M.H., Martinis J.M. (2004). "Implementing Qubits with Superconducting Integrated Circuits". Quantum Information Processing, v.3, N1. Pdf
- ↑ Raphael Tsu and Timir Datta (2008) "Conductance and Wave Impedance of Electrons". Progress In Electromagnetics Research Symposium, Hangzhou, China, March 24–28 Pdf
- ↑ Yakymakha O.L.(1989). High Temperature Quantum Galvanomagnetic Effects in the Two- Dimensional Inversion Layers of MOSFET's (In Russian). Kyiv: Vyscha Shkola. p.91. ISBN 5-11-002309-3. djvu
- 1 2 3 Yakymakha O.L., Kalnibolotskij Y.M. (1994). "Very-low-frequency resonance of MOSFET amplifier parameters". Solid- State Electronics 37(10),1739-1751 Pdf
- ↑ Serge Luryi (1988). "Quantum capacitance device". Appl.Phys.Lett. 52(6). Pdf
- ↑ Devoret M.H. (1997). "Quantum Fluctuations". Amsterdam, Netherlands: Elsevier. pp.351-386. Pdf
- ↑ Yakymakha O.L., Kalnibolotskij Y.M., Solid- State Electronics, vol.38, No.3,1995.,pp.661-671 pdf
Sources
- W. H. Louisell, "Quantum Statistical Properties of Radiation" (Wiley, New York, 1973)
- Michel H.Devoret. Quantum Fluctuation in Electric Circuit.PDF
- Fan Hong-yi, Pan Xiao-yin. Chin.Phys.Lett. No9(1998)625.PDF
- Xu, Xing-Lei; Li, Hong-Qi; Wang, Ji-Suo Quantum fluctuations of mesoscopic damped double resonance RLC circuit with mutual capacitance inductance coupling in thermal excitation state. Chinese Physics, Volume 16, Issue 8, pp. 2462–2470 (2007).
- Hong-Qi Li, Xing-Lei Xu and Ji-Suo Wang. Quantum Fluctuations of the Current and Voltage in Thermal Vacuum State for Mesoscopic Quartz Piezoelectric Crystal.
- Boris Ya. Zel’dovich. Impedance and parametric excitation of oscillators. UFN, 2008, v. 178, No 5 PDF
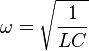

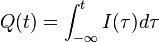
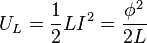
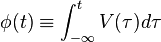

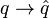
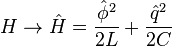
![\left[ \phi, q\right] = i\hbar](../I/m/3b4eb2ee1338d78803897f405470f542.png)
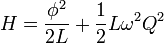
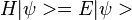
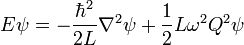
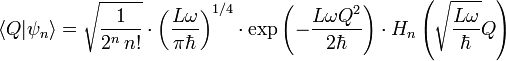
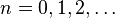
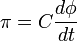
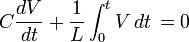
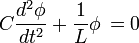
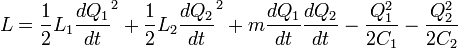
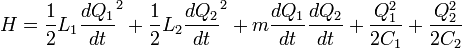
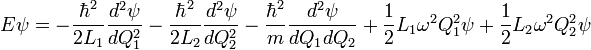
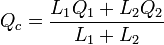

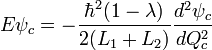
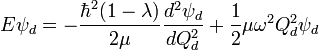
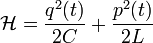
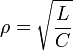
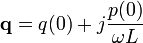
![<q(t) = Re[\mathbf{q}e^{-j\omega t}] \](../I/m/8cab017b82b55d9cec1242ed0eb8dc6c.png)
![p(t) = Im[\omega L\mathbf{q}e^{-j\omega t}] \](../I/m/bdea29d9081512e126ad3099fa44fbea.png)
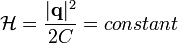
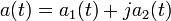

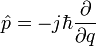
![\hat{\mathcal{H}} \hbar \omega [\hat{a}_1^2(t) + \hat {a}_2^2(t)] = \hbar \omega [\hat {a}\hat {a}^\dagger + 1/2] \](../I/m/dfd08c11754c7831d1d52a0917576fa2.png)