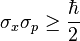Quantum Bayesianism

Quantum Bayesianism most often refers to a "subjective Bayesian account of quantum probability",[1] that has evolved primarily from the work of Caves, Fuchs and Schack (published during 2002–2013), and draws from the fields of quantum information and Bayesian probability. It is very similar to the Copenhagen interpretation that is commonly taught in textbooks.[2]

It may sometimes refer more generically to approaches to quantum theory that use a Bayesian or personalist (aka "subjective") probabilistic approach to the probabilities that appear in quantum theory. The approach associated with Caves, Fuchs, and Schack has been referred to as "the radical Bayesian interpretation" (Jaeger 2009[3]) It attempts to provide an understanding of quantum mechanics and to derive modern quantum mechanics from informational considerations. The remainder of this article concerns primarily the Caves-Fuchs-Schack Bayesian approach to quantum theory.

Quantum Bayesianism deals with common questions in the interpretation of quantum mechanics about the nature of wavefunction superposition, non-locality, and entanglement.[4][5] As the interpretation of quantum mechanics is important to philosophers of science, some compare the idea of degree of belief and its application in Quantum Bayesianism with the idea of anti-realism[1] from philosophy of science.

Fuchs and Schack have referred to their current approach to the quantum Bayesian program as "QBism". On a technical level, QBism uses symmetric, informationally-complete, positive operator-valued measures (SIC-POVMs) to rewrite quantum states (either pure or mixed) as a set of probabilities defined over the outcomes of a "Bureau of Standards" measurement.[6] That is, if one translates a density matrix into a probability distribution over the outcomes of a SIC-POVM experiment, one can reproduce all the statistical predictions (normally computed by using the Born rule) on the density matrix from the SIC-POVM probabilities instead. The Born rule then takes on the function of relating one valid probability distribution to another, rather than of deriving probabilities from something apparently more fundamental.[7] QBist foundational research stimulated interest in SIC-POVMs, which now have applications in quantum theory outside of foundational studies.[8] Likewise, a quantum version of the de Finetti theorem, introduced by Caves, Fuchs and Schack (see also Störmer, 1969 [9]) to provide a QBist understanding of the idea of an "unknown quantum state",[10] has found application elsewhere, in topics like quantum key distribution[11] and entanglement detection.[12]

Origin

In the field of probability theory, there are different interpretations of probability and different forms of statistical inference which influence the conclusions that can be made from analysis of uncertain phenomena. The two dominant approaches to statistical inference include the frequentist approach (called frequentist inference) and the Bayesian approach (called Bayesian inference). The Bayesian approach upon which Quantum Bayesianism relies generally refers to a mode of statistical inference originating in, and greatly extending, the work of Thomas Bayes in statistics and probability.

Quantum Bayesianism tries to find a new understanding of quantum mechanics by applying Bayesian inference. Any new insights into quantum mechanics are beneficial, especially in light of the recent attempts to combine quantum mechanics and general relativity into a theory of quantum gravity and the interest in quantum computation. Quantum mechanics is thought to be derivable from the principles of quantum information.

In the book Lost Causes in and beyond Physics, R. F. Streater writes, "[t]he first quantum Bayesian was von Neumann. In Die mathematischen Grundlagen der Quantenmechanik, he describes the measurement process of say the spin polarization of an electron source ...".[13] Not everyone agrees.[14]

Background

Quantum Bayesianism applies the Bayesian approach to the fundamentals of quantum mechanics. The Bayesian approach is a mode of statistical inference. It introduces the concept of "degree of belief".[15]

When the wavefunction of a system is written as a linear combination of the eigenstates of an observable such as position, the squared modulus of the coefficient of the eigenstate is the probability of obtaining the corresponding eigenvalue as the result of a measurement of that observable. Since this is probabilistic, this leads to the question of whether the universe is deterministic and how this is consistent with events being described probabilistically. Another idea which Quantum Bayesianism tries to address is whether quantum mechanical probabilities are objective or subjective, and the implications of the Born rule for either.

Other variations

Quantum Bayesianism is a derivative of the popular Copenhagen interpretation of quantum mechanics. The main difference is that QBism is more explicit about interpretation of probability.

A related attempt is to derive physics from Fisher information, described in Roy Frieden's book titled Physics from Fisher Information. However, his claims are disputed by Streater.[16]

Other approaches to quantum mechanics are broadly related in that they also treat quantum states as expressions of information, knowledge, belief, or expectation. All these approaches - including QBism - can be termed "psi-epistemic",[17] but they differ in what they consider quantum states to be information or expectations 'about', as well as in the technical features of the mathematics they employ.[18]

Comparisons have also been made between QBism and the relational quantum mechanics espoused by Carlo Rovelli and others.[19]

QBism should be distinguished from other applications of Bayesian probability in quantum physics.[20] For example, quantum computer science uses Bayesian networks, which find applications in "medical diagnosis, monitoring of processes, and genetics".[21] (A Bayesian framework is also used for neural networks.[22]) Bayesian inference has also been applied in quantum theory for updating probability densities over quantum states, [23] and MaxEnt methods have been used in similar ways.[24]

See also

References

  1. 1 2 Stairs, Allen (2011). "A loose and separate certainty: Caves, Fuchs and Schack on quantum probability one" (pdf). Studies In History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics 42 (3): 158–166. doi:10.1016/j.shpsb.2011.02.001. Retrieved April 2012.
  2. ↑ Why Current Interpretations of Quantum Mechanics are Deficient, Elliott Tammaro,
  3. ↑ Jaeger, Gregg (2009). "3.7. The radical Bayesian interpretation". Entanglement, information, and the interpretation of quantum mechanics (Online-Ausg. ed.). Berlin: Springer. pp. 170–179. ISBN 978-3-540-92127-1.
  4. ↑ Timpson, Christopher Gordon (2008). "Quantum Bayesianism: A study" (postscript). Studies In History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics 39 (3): 579–609. doi:10.1016/j.shpsb.2008.03.006. Retrieved April 2012.
  5. ↑ Mermin (2012a), Mermin (2012b)
  6. ↑ Fuchs and Schack (2011); Appleby, Ericsson and Fuchs (2011); Rosado (2011); Fuchs (2012)
  7. ↑ Fuchs and Schack (2011); Appleby, Ericsson and Fuchs (2011); Fuchs (2012)
  8. ↑ Scott (2006); Wootters and Sussman (2007); Fuchs (2012); Appleby et al. (2012)
  9. ↑ Störmer, E. (1969). "Symmetric states of infinite tensor products of C*-algebras". J. Funct. Anal. 3: 48–68. doi:10.1016/0022-1236(69)90050-0.
  10. ↑ Caves, Fuchs and Schack (2002); Baez (2007)
  11. ↑ Renner (2005)
  12. ↑ Doherty et al. (2005)
  13. ↑ Streater, R. F. (2007). Lost Causes in and beyond Physics. Springer. p. 70. ISBN 3-540-36581-8.
  14. ↑ Von Neumann Was Not a Quantum Bayesian, Blake C. Stacey,
  15. ↑ Talbott, William; Edward N. Zalta (Summer 2011). "Bayesian Epistemology". The Stanford Encyclopedia of Philosophy.
  16. ↑ Streater, R. F. (2007). Lost Causes in and beyond Physics. Springer. p. 69. ISBN 3-540-36581-8.
  17. ↑ Harrigan and Spekkens (2010)
  18. ↑ Bub and Pitowsky (2009)
  19. ↑ Marlow (2006); Smerlak and Rovelli (2007); Fuchs (2012)
  20. ↑ Fuchs and Schack (2013), footnote 3; Baez (2003).
  21. ↑ Tucci, Robert (17 Jun 1997). "Quantum Bayesian Nets". Int. Jour. Of Mod. Phys.
  22. ↑ MacKay, David (May 1992). "A Practical Bayesian Framework for Backpropagation Networks". Neural Computation 4: 448–472. doi:10.1162/neco.1992.4.3.448. Retrieved 30 April 2012.
  23. ↑ Jones (1991)
  24. ↑ Baez (2003), Canosa et al. (1992), Bužek et al. (1998).

Further reading

External links

This article is issued from Wikipedia - version of the Thursday, January 28, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.