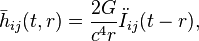Quadrupole formula
In general relativity, the quadrupole formula describes rate at which gravitational waves are emitted from a system of masses based on the change of the (mass) quadrupole moment. The formula reads
where 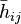 is the (spatial part of) the trace reversed perturbation of the metric (i.e. the gravitational wave), and
is the (spatial part of) the trace reversed perturbation of the metric (i.e. the gravitational wave), and 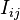 is the mass quadrupole moment.[1]
is the mass quadrupole moment.[1]
The formula was first obtained by Albert Einstein in 1916. After a long history of debate on its physical correctness, observations of energy loss due to gravitational radiation in the Hulse–Taylor binary discovered in 1974 confirmed the result, with agreement up to 0.2 percent (by 2005).[2]
References
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This article is issued from Wikipedia - version of the Friday, February 27, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.