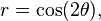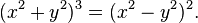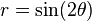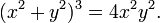Quadrifolium

Rotated Quadrifolium
This article is about the geometric shape. For the plant, see Four-leaf clover. For the symmetrical shape framework, see Quatrefoil.
The quadrifolium (also known as four-leaved clover[1]) is a type of rose curve with n=2. It has polar equation:
with corresponding algebraic equation
Rotated by 45°, this becomes
with corresponding algebraic equation
In either form, it is a plane algebraic curve of genus zero.
The dual curve to the quadrifolium is
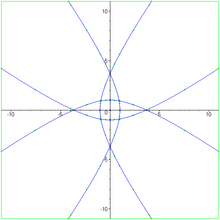
Dual Quadrifolium
The area inside the curve is 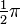 , which is exactly half of the area of the circumcircle of the quadrifolium. The length of the curve is ca. 9.6884.[2]
, which is exactly half of the area of the circumcircle of the quadrifolium. The length of the curve is ca. 9.6884.[2]
Notes
- ↑ C G Gibson, Elementary Geometry of Algebraic Curves, An Undergraduate Introduction, Cambridge University Press, Cambridge, 2001, ISBN 978-0-521-64641-3. Pages 92 and 93
- ↑ Quadrifolium - from Wolfram MathWorld
References
- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. p. 175. ISBN 0-486-60288-5.
External links
This article is issued from Wikipedia - version of the Sunday, March 01, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.