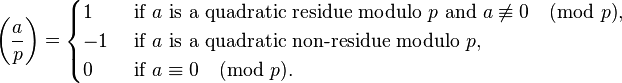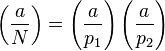Quadratic residuosity problem

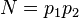The quadratic residuosity problem in computational number theory is to decide, given integers $a$ and $N$ , whether $a$ is a quadratic residue modulo $N$ or not. Here $N = p_1 p_2$ for two unknown primes $p_1$ and $p_2$ , and $a$ is among the numbers which are not obviously quadratic non-residues (see below).

The problem was first described by Gauss in his Disquisitiones Arithmeticae in 1801. This problem is believed to be computationally difficult. Several cryptographic methods rely on its hardness, see Applications.

An efficient algorithm for the quadratic residuosity problem immediately implies efficient algorithms for other number theoretic problems, such as deciding whether a composite $N$ of unknown factorization is the product of 2 or 3 primes .^[1]

Precise formulation

Given integers $a$ and $T$ , $a$ is said to be a quadratic residue modulo $T$ if there exists an integer $b$ such that

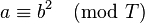a \equiv b^2 \pmod T

Otherwise we say it is a quadratic non-residue. When 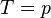$T = p$ is a prime, it is customary to use the Legendre symbol:

\left(\frac{a}{p}\right) = \begin{cases} 1 & \text{ if } a \text{ is a quadratic residue modulo } p \text{ and } a \not\equiv 0\pmod{p}, \\ -1 & \text{ if } a \text{ is a quadratic non-residue modulo } p, \\ 0 & \text{ if } a \equiv 0 \pmod{p}. \end{cases}

This is a multiplicative character which means 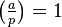$\big(\tfrac{a}{p}\big) = 1$ for exactly 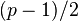$(p-1)/2$ of the values 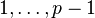$1,\ldots,p-1$ , and it is 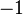$-1$ for the remaining.

It is easy to compute using the law of quadratic reciprocity in a manner akin to the Euclidean algorithm, see Legendre symbol.

Consider now some given 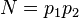$N = p_1 p_2$ where $p_1$ and $p_2$ are two, different unknown primes. A given $a$ is a quadratic residue modulo $N$ if and only if $a$ is a quadratic residue modulo both $p_1$ and $p_2$ .

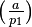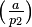Since we don't know $p_1$ or $p_2$ , we cannot compute $\big(\tfrac{a}{p_1}\big)$ and $\big(\tfrac{a}{p_2}\big)$ . Perhaps surprisingly, however, we can easily compute their product! This is known as the Jacobi symbol:

\left(\frac{a}{N}\right) = \left(\frac{a}{p_1}\right)\left(\frac{a}{p_2}\right)

This can also be efficiently computed using the law of quadratic reciprocity for Jacobi symbols.

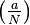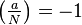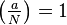However, $\big(\tfrac{a}{N}\big)$ can not in all cases tell us whether $a$ is a quadratic residue modulo $N$ or not! More precisely, if $\big(\tfrac{a}{N}\big) = -1$ then $a$ is necessarily a quadratic non-residue modulo either $p_1$ or $p_2$ , in which case we are done. But if $\big(\tfrac{a}{N}\big) = 1$ then it is either the case that $a$ is a quadratic residue modulo both $p_1$ and $p_2$ , or a quadratic non-residue modulo both $p_1$ and $p_2$ . 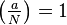We cannot distinguish these cases from knowing just that $\big(\tfrac{a}{N}\big) = 1$ .

This leads to the precise formulation of the quadratic residue problem:

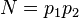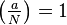Problem: Given integers $a$ and $N = p_1 p_2$ , where $p_1$ and $p_2$ are unknown, different primes, and where $\big(\tfrac{a}{N}\big) = 1$ , determine whether $a$ is a quadratic residue modulo $N$ or not.

Equal Distribution

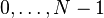If $a$ is drawn uniformly at random among those integers from $0,\ldots,N-1$ which satisfy 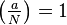$\big(\tfrac{a}{N}\big) = 1$ , is $a$ more often a quadratic residue or a quadratic non-residue modulo $N$ ?

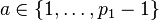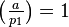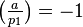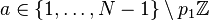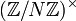As earlier mentioned, for exactly half of the choices of $a \in \{1,\ldots,p_1-1\}$ , then $\big(\tfrac{a}{p_1}\big) = 1$ , and for the rest we have $\big(\tfrac{a}{p_1}\big) = -1$ . By extension, this also holds for half the choices of $a \in \{1,\ldots,N-1\} \setminus p_1\mathbb{Z}$ . Similarly for $p_2$ . 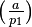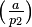Using basic algebra, it is easy to show that this divides $(\mathbb{Z}/N\mathbb{Z})^\times$ into 4 equal parts, depending on the sign of $\big(\tfrac{a}{p_1}\big)$ and $\big(\tfrac{a}{p_2}\big)$ .

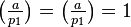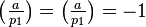The allowed $a$ in the quadratic residue problem given as above constitute exactly those two parts corresponding to the cases $\big(\tfrac{a}{p_1}\big) = \big(\tfrac{a}{p_1}\big) = 1$ and $\big(\tfrac{a}{p_1}\big) = \big(\tfrac{a}{p_1}\big) = -1$ . Consequently, exactly half of the possible $a$ are quadratic residues and the remaining are not.

Applications

The intractability of the quadratic residuosity problem is the basis for the security of the Blum Blum Shub pseudorandom number generator and the Goldwasser–Micali cryptosystem.^[2]^[3]

Notes

↑ Adleman, L. (1980). "On Distinguishing Prime Numbers from Composite Numbers". Proceedings of the 21st IEEE Symposium on the Foundations of Computer Science (FOCS), Syracuse, N.Y. pp. 387–408.
↑ S. Goldwasser, S. Micali (1982). "Probabilistic encryption and how to play mental poker keeping secret all partial information". Proc. 14th Symposium on Theory of Computing: 365–377. doi:10.1145/800070.802212.
↑ S. Goldwasser, S. Micali (1984). "Probabilistic encryption". Journal of Computer and System Sciences 28 (2): 270–299. doi:10.1016/0022-0000(84)90070-9.

This article is issued from Wikipedia - version of the Thursday, August 27, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Quadratic residuosity problem

Precise formulation

Equal Distribution

Applications

See also

Notes