Quadratic integral

In mathematics, a quadratic integral is an integral of the form

\int \frac{dx}{a+bx+cx^2}.

It can be evaluated by completing the square in the denominator.

\int \frac{dx}{a+bx+cx^2} = \frac{1}{c} \int \frac{dx}{\left( x+ \frac{b}{2c} \right)^2 + \left( \frac{a}{c} - \frac{b^2}{4c^2} \right)}.

Positive-discriminant case

Assume that the discriminant q = b2 − 4ac is positive. In that case, define u and A by

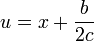u = x + \frac{b}{2c} ,

and

-A^2 = \frac{a}{c} - \frac{b^2}{4c^2} = \frac{1}{4c^2} \left( 4ac - b^2 \right).

The quadratic integral can now be written as

\int \frac{dx}{a+bx+cx^2} = \frac1c \int \frac{du}{u^2-A^2} = \frac1c \int \frac{du}{(u+A)(u-A)}.

The partial fraction decomposition

\frac{1}{(u+A)(u-A)} = \frac{1}{2A} \left( \frac{1}{u-A} - \frac{1}{u+A} \right)

allows us to evaluate the integral:

\frac1c \int \frac{du}{(u+A)(u-A)} = \frac{1}{2Ac} \ln \left( \frac{u - A}{u + A} \right) + \text{constant}.

The final result for the original integral, under the assumption that q > 0, is

\int \frac{dx}{a+bx+cx^2} = \frac{1}{ \sqrt{q}} \ln \left( \frac{2cx + b - \sqrt{q}}{2cx+b+ \sqrt{q}} \right) + \text{constant, where } q = b^2 - 4ac.

Negative-discriminant case

This (hastily written) section may need attention.

In case the discriminant q = b2 − 4ac is negative, the second term in the denominator in

\int \frac{dx}{a+bx+cx^2} = \frac{1}{c} \int \frac{dx}{\left( x+ \frac{b}{2c} \right)^2 + \left( \frac{a}{c} - \frac{b^2}{4c^2} \right)}.

is positive. Then the integral becomes

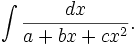
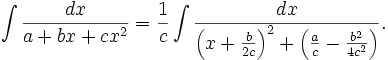
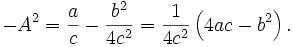
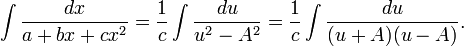
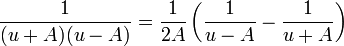
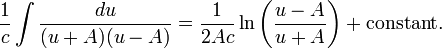
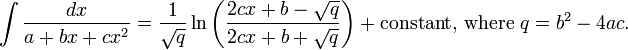
\begin{align} & {} \qquad \frac{1}{c} \int \frac{ du} {u^2 + A^2} \\[9pt] & = \frac{1}{cA} \int \frac{du/A}{(u/A)^2 + 1 } \\[9pt] & = \frac{1}{cA} \int \frac{dw}{w^2 + 1} \\[9pt] & = \frac{1}{cA} \arctan(w) + \mathrm{constant} \\[9pt] & = \frac{1}{cA} \arctan\left(\frac{u}{A}\right) + \text{constant} \\[9pt] & = \frac{1}{c\sqrt{\frac{a}{c} - \frac{b^2}{4c^2}}} \arctan \left(\frac{x + \frac{b}{2c}}{\sqrt{\frac{a}{c} - \frac{b^2}{4c^2}}}\right) + \text{constant} \\[9pt] & = \frac{2}{\sqrt{4ac - b^2\, }} \arctan\left(\frac{2cx + b}{\sqrt{4ac - b^2}}\right) + \text{constant}. \end{align}

References

This article is issued from Wikipedia - version of the Saturday, March 23, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.