Pushforward (homology)
In algebraic topology, the pushforward of a continuous function  :
:  between two topological spaces is a homomorphism
between two topological spaces is a homomorphism 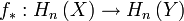 between the homology groups for
between the homology groups for 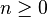 .
.
Homology is a functor which converts a topological space  into a sequence of homology groups
into a sequence of homology groups 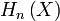 . (Often, the collection of all such groups is referred to using the notation
. (Often, the collection of all such groups is referred to using the notation 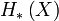 ; this collection has the structure of a graded ring.) In any category, a functor must induce a corresponding morphism. The pushforward is the morphism corresponding to the homology functor.
; this collection has the structure of a graded ring.) In any category, a functor must induce a corresponding morphism. The pushforward is the morphism corresponding to the homology functor.
Definition for singular and simplicial homology
We build the pushforward homomorphism as follows (for singular or simplicial homology):
First we have an induced homomorphism between the singular or simplicial chain complex 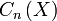 and
and 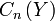 defined by composing each singular n-simplex
defined by composing each singular n-simplex  :
: 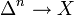 with
with  to obtain a singular n-simplex of
to obtain a singular n-simplex of 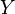 ,
, 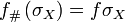 :
: 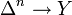 . Then we extend
. Then we extend 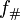 linearly via
linearly via 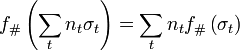 .
.
The maps 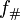 :
:  satisfy
satisfy 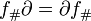 where
where 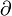 is the boundary operator between chain groups, so
is the boundary operator between chain groups, so 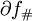 defines a chain map.
defines a chain map.
We have that 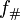 takes cycles to cycles, since
takes cycles to cycles, since 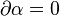 implies
implies 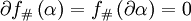 . Also
. Also 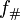 takes boundaries to boundaries since
takes boundaries to boundaries since 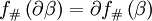 .
.
Hence 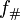 induces a homomorphism between the homology groups
induces a homomorphism between the homology groups 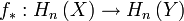 for
for 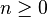 .
.
Properties and homotopy invariance
Two basic properties of the push-forward are:
-
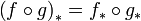 for the composition of maps
for the composition of maps 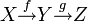 .
. -
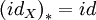 where
where 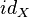 :
: 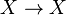 refers to identity function of
refers to identity function of  and
and 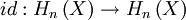 refers to the identity isomorphism of homology groups.
refers to the identity isomorphism of homology groups.
A main result about the push-forward is the homotopy invariance: if two maps 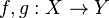 are homotopic, then they induce the same homomorphism
are homotopic, then they induce the same homomorphism 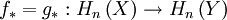 .
.
This immediately implies that the homology groups of homotopy equivalent spaces are isomorphic:
The maps 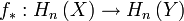 induced by a homotopy equivalence
induced by a homotopy equivalence  :
:  are isomorphisms for all
are isomorphisms for all  .
.
References
- Allen Hatcher, Algebraic topology. Cambridge University Press, ISBN 0-521-79160-X and ISBN 0-521-79540-0